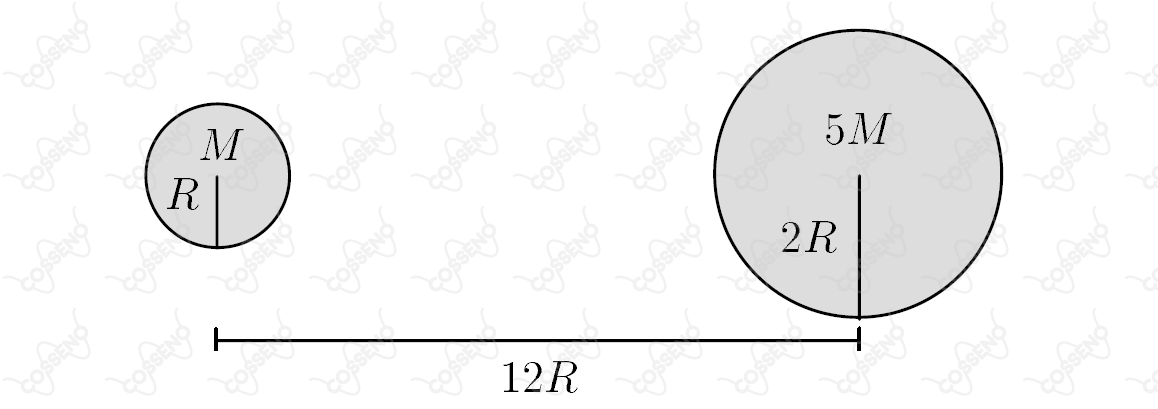
Dois corpos esféricos de massa e e raios e , respectivamente, são liberados no espaço livre. Considerando que a única força interveniente seja a da atração gravitacional mútua, e que seja de a distância de separação inicial entre os centros dos corpos, então, o espaço percorrido pelo corpo menor até a colisão será de
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A princípio, veja que a distância de colisão é $9R$, devido os raios das esferas. Nesse sentido, podemos pensar em duas partículas distando $9R$ uma da outra, tal que como o sistema é isolado, podemos aplicar a conservação da quantidade de movimento, isto é:\begin{matrix}
p_{inicial} = p_{final}\\ \\ \underbrace{M(0) + 5M(0)}_{\text{partem do respouso}} = M(v_1) + 5M(-v_2) \\ v_1 = 5v_2
\end{matrix}Para um mesmo intervalo de tempo, pode-se dizer que:\begin{matrix} \Delta x_1 = 5 \Delta x_2
\end{matrix}Já pensando na colisão, ambos os corpos devem percorrer $9R$, logo:\begin{matrix}\Delta x_1 + \Delta x_2 = 9R &\therefore& \boxed{\Delta x_1 = 7,5R}
\end{matrix}\begin{matrix}Letra \ (D)
\end{matrix}$\color{orangered}{\text{Obs:}}$ O índice $1$ foi utilizado para o corpo esférico menor, assim como o $2$ para o maior.

