Considere o vão existente entre cada tecla de um computador e a base do seu teclado. Em cada vão existem duas placas metálicas, uma delas presa na base do teclado e a outra, na tecla. Em conjunto, elas funcionam como um capacitor de placas planas paralelas imersas no ar. Quando se aciona a tecla, diminui a distância entre as placas e a capacitância aumenta. Um circuito elétrico detecta a variação da capacitância, indicativa do movimento da tecla. Considere então um dado teclado, cujas placas metálicas têm de área e de distância inicial entre si. Considere ainda que a permissividade do ar seja .
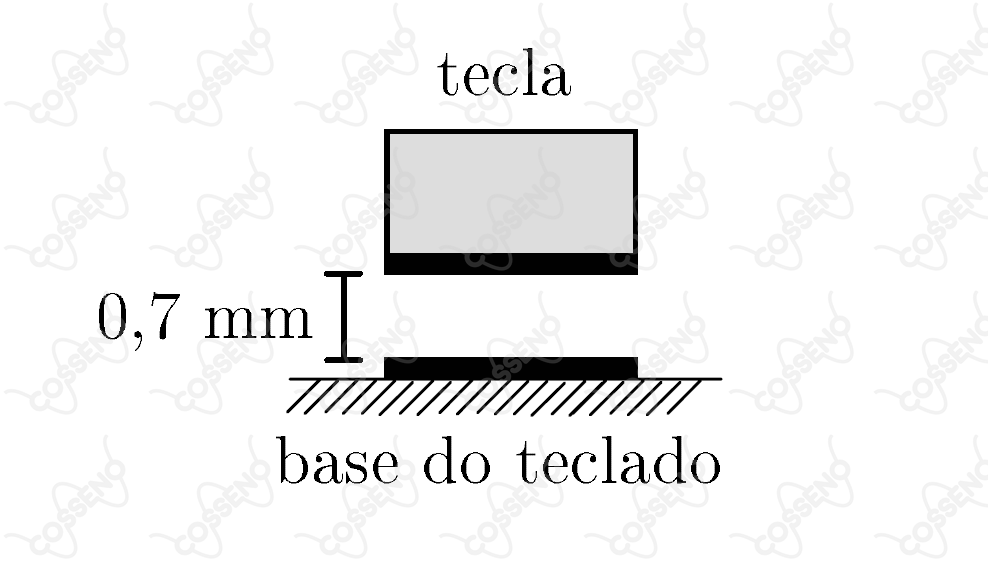
Se o circuito eletrônico é capaz de detectar uma variação da capacitância a partir de , então, qualquer tecla deve ser deslocada de pelo menos
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Pensando na diferença de capacitâncias, pode-se escrever:\begin{matrix}\Delta C = \varepsilon_0 A \left( \dfrac{1}{d_1} - \dfrac{1}{d_0} \right)
\end{matrix}Analisando a expressão, podemos tentar facilitar as contas, isto é, passar a constante de $\pu{F/m}$ para $\pu{F/mm}$, ou seja:\begin{matrix} \varepsilon_0 = 9 \times 10^{-15} \ \pu{F/mm}
\end{matrix}Nesse sentido, resta apenas substituir os demais dados do enunciado na expressão:\begin{matrix}(0,2 \cdot 10^{-12}) = (9 \cdot 10^{-15} )(40)\left( \dfrac{1}{d_1} - \dfrac{1}{0,7} \right) \\
\left( \dfrac{1}{d_1} - \dfrac{1}{0,7} \right) = \dfrac{10}{18} \\ \\ \boxed{d_1 = 5 \ \pu{mm}}
\end{matrix}Atente que esta é a distância mínima entre as placas, para o deslocamento mínimo, têm-se:\begin{matrix}\boxed{d_0 - d_1 = 0,2 \ \pu{mm}} \\ \\ Letra \ (B)
\end{matrix}

