Um pescador deixa cair uma lanterna acesa em um lago a $10{,}0\text{ m}$ de profundidade. No fundo do lago, a lanterna emite um feixe luminoso formando um pequeno ângulo $\theta$ com a vertical (veja figura).
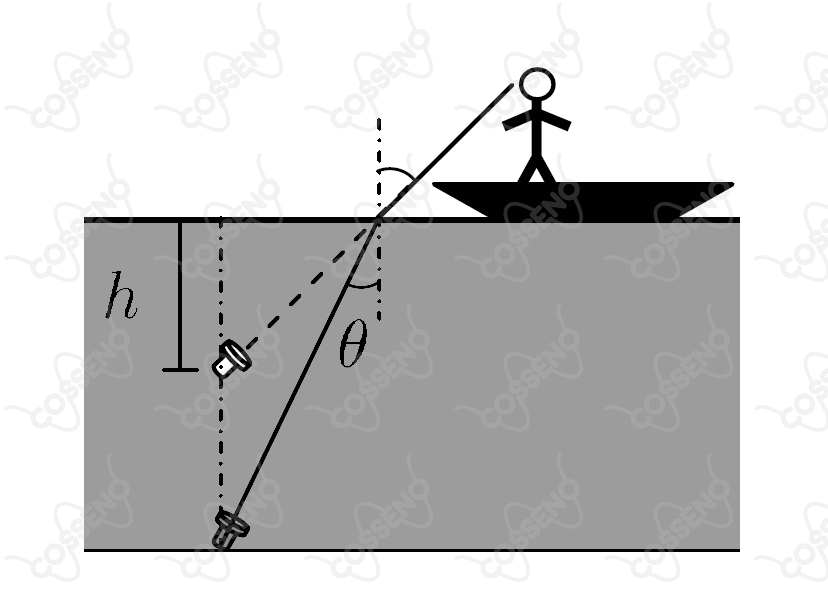
Considere: $\tan \theta \simeq \sin \theta \simeq \theta$ é o índice de refração da agua $n = 1{,}33$. Então, a profundidade aparente $h$ vista pelo pescador é igual a
A questão é basicamente a aplicação do $\text{Dióptro Plano}$, entretanto, caso você não soubesse, o enunciado deixa diversas informações que contribuiriam para uma rápida solução, veja:
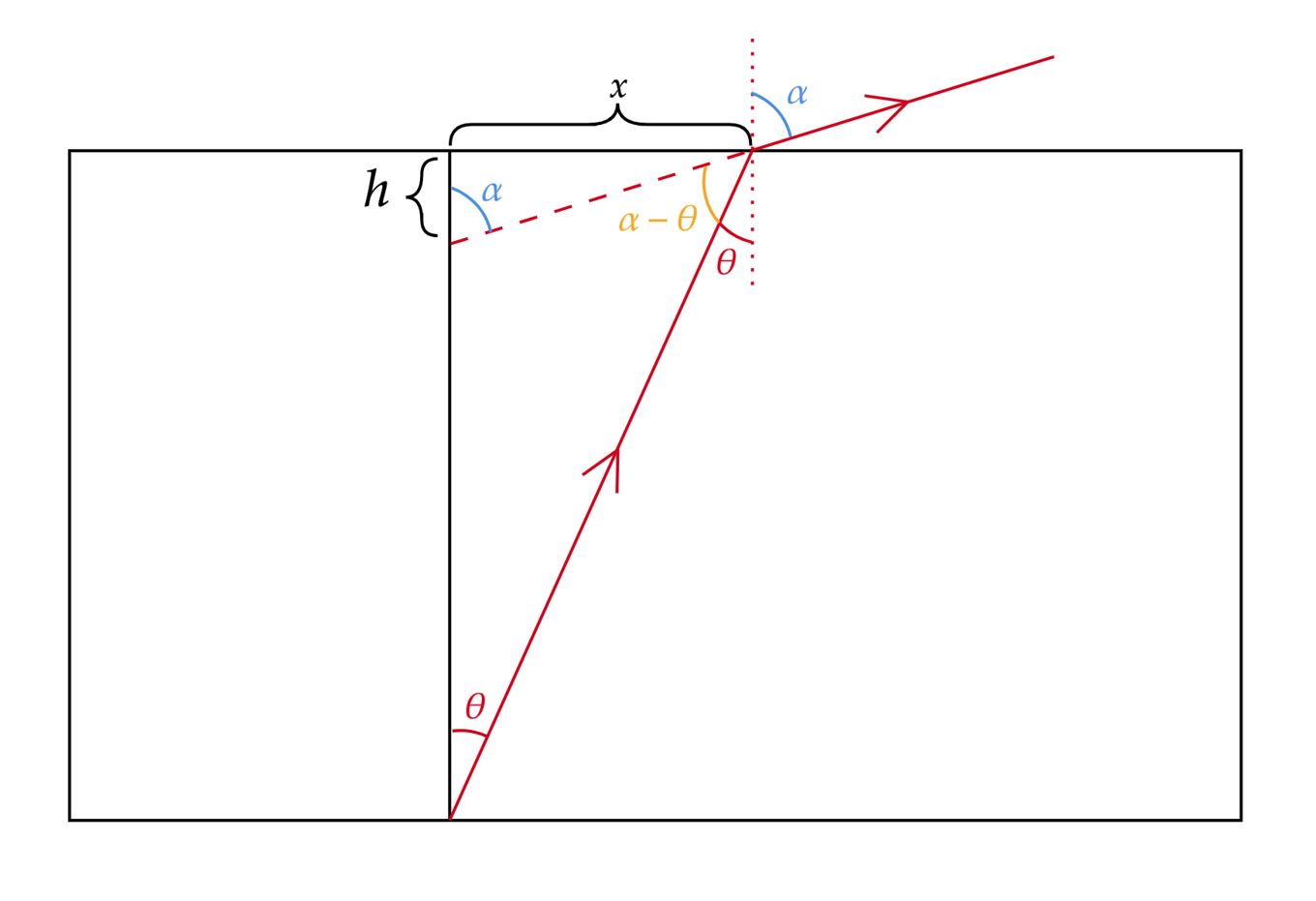Da trigonometria do problema, temos: \begin{matrix} \tan{\theta} \approx \sin{\theta} \approx {\dfrac{x}{10}} &,& \tan{\alpha} \approx \sin{\alpha} \approx {\dfrac{x}{h}}
\end{matrix}Com conhecimento da $\text{Lei de Snell-Descartes}$: \begin{matrix} {\dfrac{\sin{\theta}}{\sin{\alpha}} = \dfrac{n_{ar}}{n}} &\Rightarrow& {\dfrac{h}{10} = \dfrac{n_{ar}}{n}} &\Rightarrow& \fbox{$h \approx 7,5 \ \pu{m}$}
\end{matrix} $\color{orangered}{Obs:}$ $n_{ar} \approx 1$ \begin{matrix} Letra \ (C)
\end{matrix}
Ampliar Imagem
