Um projetil de densidade é lançado com um ângulo em relação à horizontal no interior de um recipiente vazio. A seguir, o recipiente é preenchido com um superfluido de densidade , e o mesmo projetil é novamente lançado dentro dele, só que sob um ângulo em relação à horizontal. Observa-se, então, que, para uma velocidade inicial do projetil, de mesmo módulo que a do experimento anterior, não se altera a distância alcançada pelo projétil (veja figura).
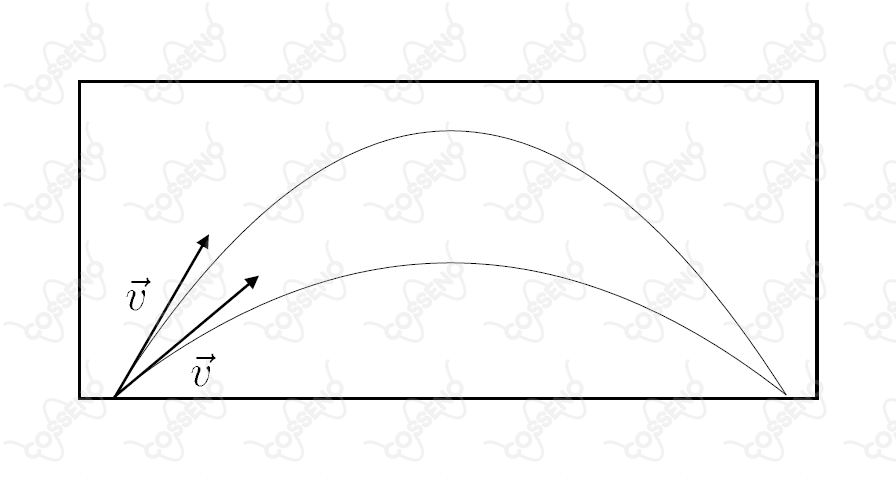
Sabendo que são nulas as forças de atrito num superfluido, podemos então afirmar, com relação ao ângulo de lançamento do projétil, que
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A princípio, note que a aceleração que irá agir nos projéteis será diferente nos dois casos. Nesse sentido, no primeiro lançamento, temos apenas a aceleração da gravidade, contudo, no segundo, há o empuxo, em que podemos escrever:\begin{matrix}ma = mg - \rho_s gV &\Rightarrow&
\rho_p V a = \rho_p Vg - \rho_s gV &\therefore& a = g\left( 1 - \dfrac{\rho_s}{\rho_p}\right)
\end{matrix}Como os alcances horizontais são os mesmos, têm-se:\begin{matrix}
A_{\alpha} = A_{\beta} \\ (v\cos{\alpha})T_{\alpha} = (v\cos{\beta})T_{\beta} \end{matrix}Observe que $T$ é tempo de percurso dos projéteis, no caso, o dobro do tempo de subida ou da queda dos projéteis (ambos equivalentes nesse caso). Desse modo, podemos escrever:\begin{matrix}
\cos{\alpha} \left( \dfrac{2v\sin{\alpha}}{g} \right) = \cos{\beta} \left( \dfrac{2v\sin{\beta}}{a} \right) \\ \\
\dfrac{2\sin{\beta}\cos{\beta}}{2\sin{\alpha}\cos{\alpha}} = \dfrac{a}{g} \\ \\
\boxed{\sin{2\beta} = \sin{2\alpha} \left( 1 - \dfrac{\rho_s}{\rho_p}\right) }
\end{matrix}\begin{matrix}Letra \ (B)
\end{matrix}$\color{orangered}{\text{Obs:}}$ Para encontrar o tempo de percurso do projétil, basta usar uma das equações horárias no eixo vertical. Nesse contexto, pensando na subida, com sentido positivo para cima, podemos escrever:\begin{matrix} v_f = v\sin{\theta} - a\dfrac{T}{2} &,& v_f = 0 &\therefore&T = \dfrac{2v\sin{\theta}}{a}
\end{matrix}

