Considere um pêndulo de comprimento , tendo na sua extremidade uma esfera de massa com uma carga elétrica positiva .
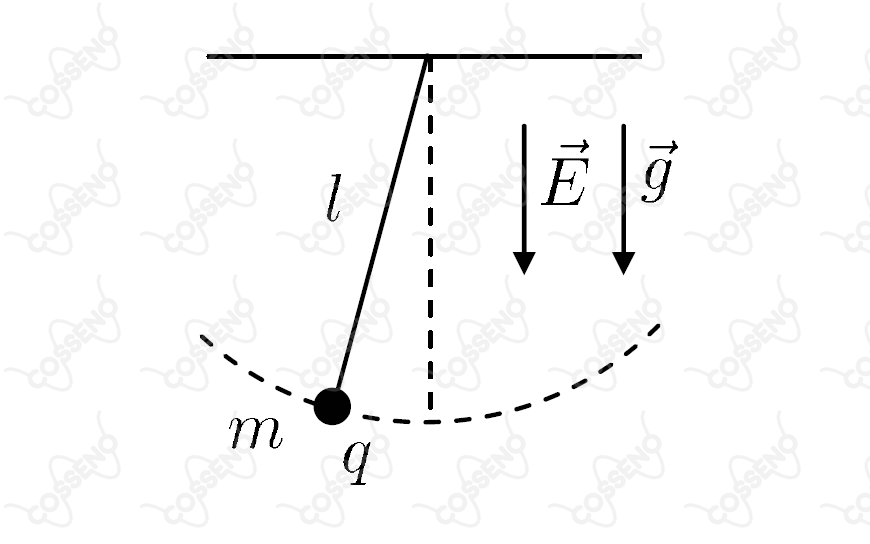
A seguir, esse pêndulo é colocado num campo elétrico uniforme que atua na mesma direção e sentido da aceleração da gravidade . Deslocando-se essa carga ligeiramente de sua posição de equilíbrio e soltando-a, ela executa um movimento harmônico simples, cujo período é
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Na situação ilustrada, a esfera de massa $m$ está sujeita a uma gravidade aparente $(a)$, em vista da presença do campo elétrico. Dessa forma, podemos encontrar a gravidade aparente por uma resultante $(F_a)$:
\begin{matrix} F_a = P + F_{ele} &\Rightarrow& ma = mg + Eq &\Rightarrow& \fbox{$a = {\dfrac{mg+Eq}{m}}$}
\end{matrix}Com conhecimento da equação do período de um pêndulo simples, temos: \begin{matrix} T = 2\pi \ \sqrt{{ \dfrac{l}{a}}} &\Rightarrow& \fbox{$T = 2\pi \ \sqrt{{ \dfrac{l m}{mg+ qE}}}$}
\end{matrix}
\begin{matrix} Letra \ (E)
\end{matrix}

13:24 14/08/2023
Bom dia! Porque não houve a necessidade de analisar a força do cabo sobre a carga na resultante das forças?

19:59 14/08/2023
Boa tarde, Leandro! Repare que utilizei "resultante das forças" não para todas as forças que atuam no pêndulo, mas, sim, aquelas que compõem a gravidade aparente! (Creio que seja essa a confusão, vou corrigir aqui).
Seja $g_{ap}$ a gravidade aparente , $a_{p}$ a aceleração ocasionada pela força peso $P$ , $a_{e}$ a aceleração ocasionada pela força elétrica $F_{e}$ e $T$ o período desejado.
Sabemos que $T = \sqrt{\dfrac{l}{g_{ap}}}$ , note que como a força $P$ e a força $F_{e}$ têm a mesma direção e sentido , temos que $g_{ap} = a_{p} +a_{e} $
Cálculo de $a_{p} $:
$P = m \cdot a_{p} = m \cdot g \implies \boxed{ a_{p} = g}$
Cálculo de $a_{e} $:
$F_{e} = m \cdot a_{e} = qE \implies \boxed{a_{e} = \dfrac{qE}{m}} $
$\therefore$
$g_{ap} = a_{p} +a_{e} = g + \dfrac{qE}{m} \implies \boxed{g_{ap} = \dfrac{mg + qE}{m}}$
$\therefore$
$T= \sqrt{\dfrac{l}{g_{ap}}} = \boxed{T =\sqrt{\dfrac{ml}{(mg + qE)}} }$
$\text{Resposta : Alternativa E}$

