A princípio, é necessário ter conhecimento da "Rosa dos Ventos", ou ao menos saber que os pontos colaterais distam $45º$ dos eixos. Nesse sentido, pensando na vista superior da situação, conseguimos esboçar: 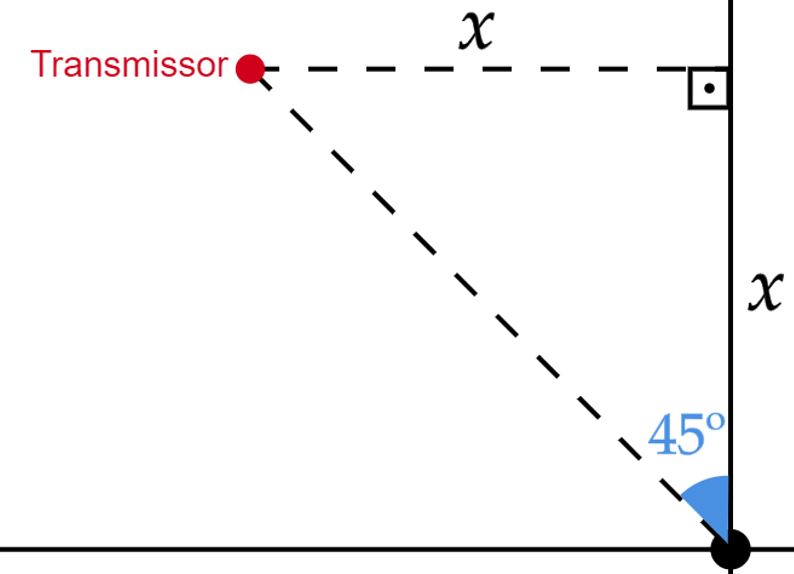Não é difícil perceber que o triângulo formado é isósceles, assim, vamos encontrar a distância $x$ percorrida pelo avião a partir de uma equação horária do $\text{MRUV}$:\begin{matrix} x = (50\sqrt{10}) \left( \dfrac{40\sqrt{10}}{3}\right) + \dfrac{6}{2}\left( \dfrac{40\sqrt{10}}{3}\right)^2 \\ x = 12.000 \ \pu{m} \\ \boxed{x =12 \ \pu{km}} \end{matrix}Observe que esta não é a distância do avião ao transmissor, mas sim a distância do solo que os separa. Nesse sentido, como o avião está voando a uma altura de $5,0 \ \pu{km}$, é possível imaginar: 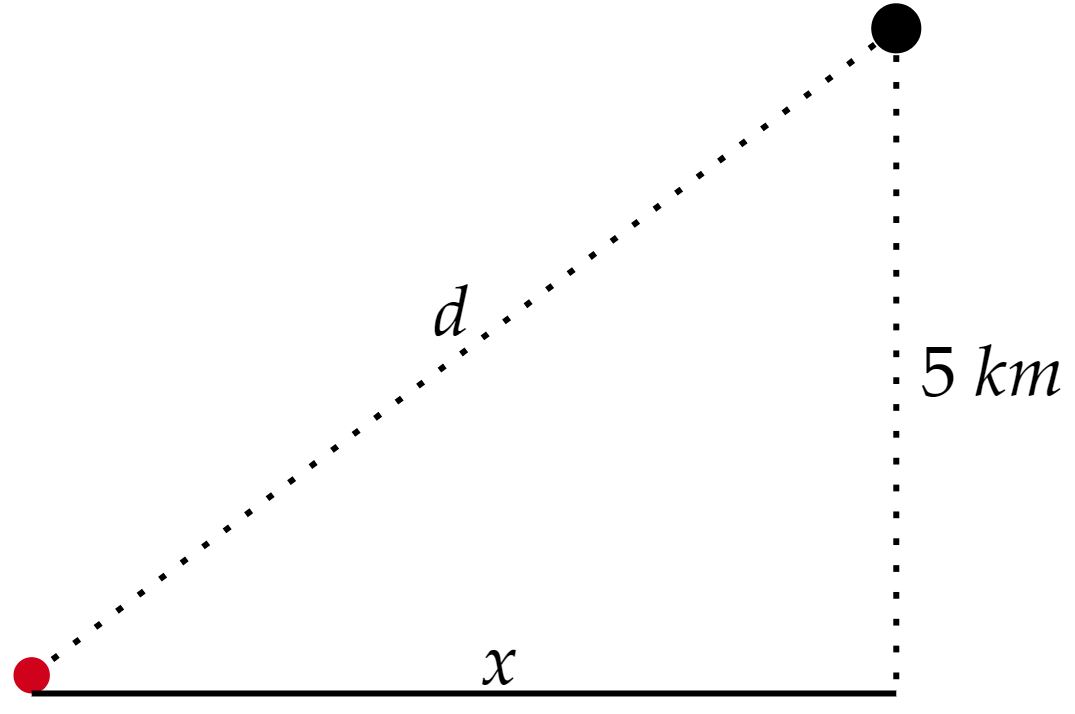Por fim, resta apenas aplicar o teorema de Pitágoras:\begin{matrix}d^2 = x^2 + 5^2 &\therefore& \boxed{d = 13 \ \pu{km}} \end{matrix}\begin{matrix}Letra \ (D) \end{matrix}