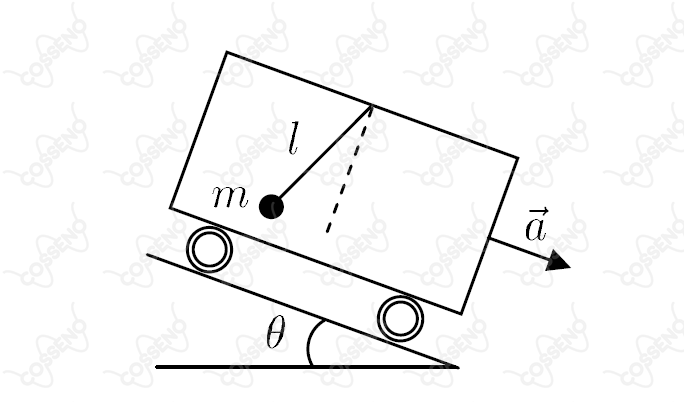
Considere uma rampa de ângulo com a horizontal sobre a qual desce um vagão, com aceleração , em cujo teto está dependurada uma mola de comprimento , de massa desprezível e constante de mola , tendo uma massa fixada na sua extremidade. Considerando que é o comprimento natural da mola e que o sistema está em repouso com relação ao vagão, pode-se dizer que a mola sofreu uma variação de comprimento dada por
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Como o sistema massa mola está inclinado em relação ao solo e submetido a uma aceleração podemos decompor as forças atuantes sobre a massa em uma componente paralela à rampa $F_1$ e outra perpendicular $F_2$:
$$F_1=m(g\sin\theta-a)\ \ \text{e}\ \ F_2=mg\cos\theta$$
A força resultante é dada por:
$$F_R=\sqrt{F_1^2+F_2^2}=m\sqrt{a^2-2a\sin\theta+g^2}$$
Daí temos a deformação da mola em função dos parâmetros:
$$m\sqrt{a^2-2a\sin\theta+g^2}/k$$
$$Letra\ E$$

