A priori, imaginando e esboçando a situação, têm-se algo como: 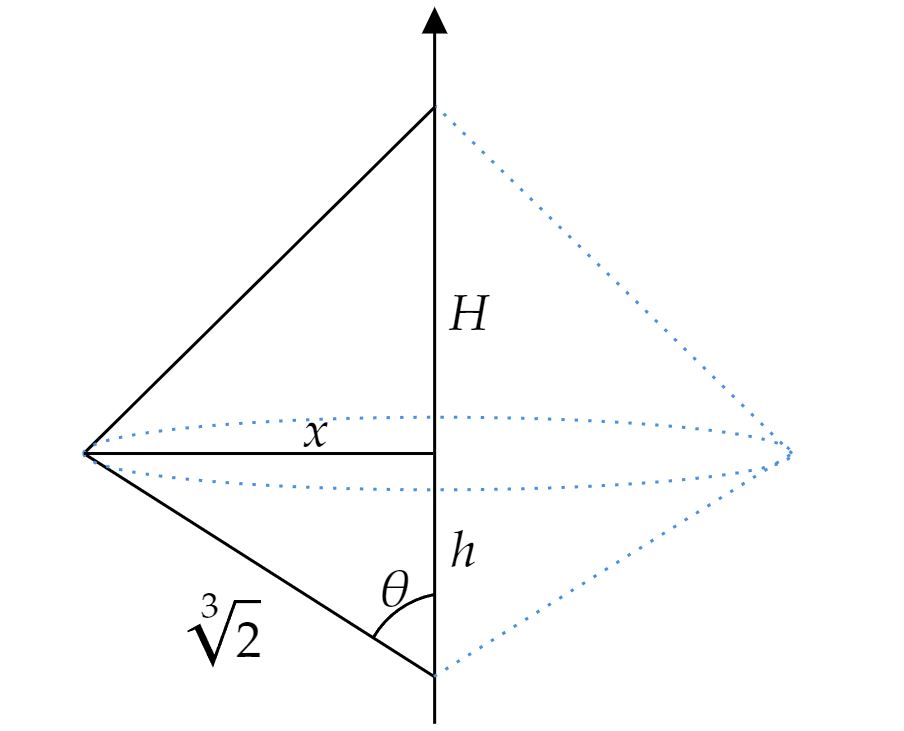Repare que, o sólido em questão é a composição de dois cones, assim, o volume deste sólido é: \begin{matrix} V = {{\dfrac{h}{3}}}\cdot (\pi x^2) + {{\dfrac{H}{3}}}\cdot (\pi x^2) = \pi &\therefore& x^2 \cdot (h+H) = 3 & (1) \end{matrix}Observe a figura novamente, dela, pode-se encontrar: \begin{matrix} \cos{\theta} = {{\dfrac{\sqrt[3]{2}}{(h+H)}}} &\Rightarrow& (h+H) = {{\dfrac{\sqrt[3]{2}}{ \cos{\theta}}}} \\ \\ \sin{\theta} = {{\dfrac{x}{\sqrt[3]{2}}}} &\Rightarrow&x = \sqrt[3]{2} \cdot \sin{\theta} \end{matrix}Substituindo os resultado acima em $(1)$: \begin{matrix} (\sqrt[3]{2} \cdot \sin{\theta})^2 \cdot {{\dfrac{\sqrt[3]{2}}{ \cos{\theta}}}} = 3 &\therefore& \sin^2{\theta} = {{\dfrac{3}{2}}}\cdot \cos{\theta} & (2) \end{matrix}Conhecida a relação fundamental da trigonometria, e substituindo $(2)$ nela, têm-se: \begin{matrix} \sin^2{\theta} + \cos^2{\theta} = 1 &\Rightarrow& \cos^2{\theta} + {{\dfrac{3}{2}}}\cos{\theta} - 1 = 0 &\therefore& \cos{\theta} = {{\dfrac{1}{2}}} &\Rightarrow& \fbox{$ \theta = 60^{\circ}$} \end{matrix}Como o triângulo é retângulo, seus ângulos devem ser na forma:\begin{matrix}90^{\circ} - \theta &,& \theta &,& 90^{\circ} \end{matrix}Portanto, os ângulos serão:\begin{matrix}30^{\circ} &,& 60^{\circ} &,& 90^{\circ} & \tiny{\blacksquare} \end{matrix}