A priori, o enunciado informa que o tetraedro é regular, assim, espera-se que todas as arestas possuam a mesma medida. Nessa perspectiva, aplicando a $\text{Distância Euclidiana}$ entre os pontos, percebe-se que todas as distâncias são iguais, veja: \begin{matrix} \overline{AB} = \overline{AC} = \overline{BC} = 2\sqrt{2} \end{matrix}Com isso, pense num tetraedro regular de aresta $L$, comecemos encontrando a distância de seu vértice da base até o baricentro, distância essa que será $2x$, por conseguinte, a altura do triângulo da base será $3x$, então: 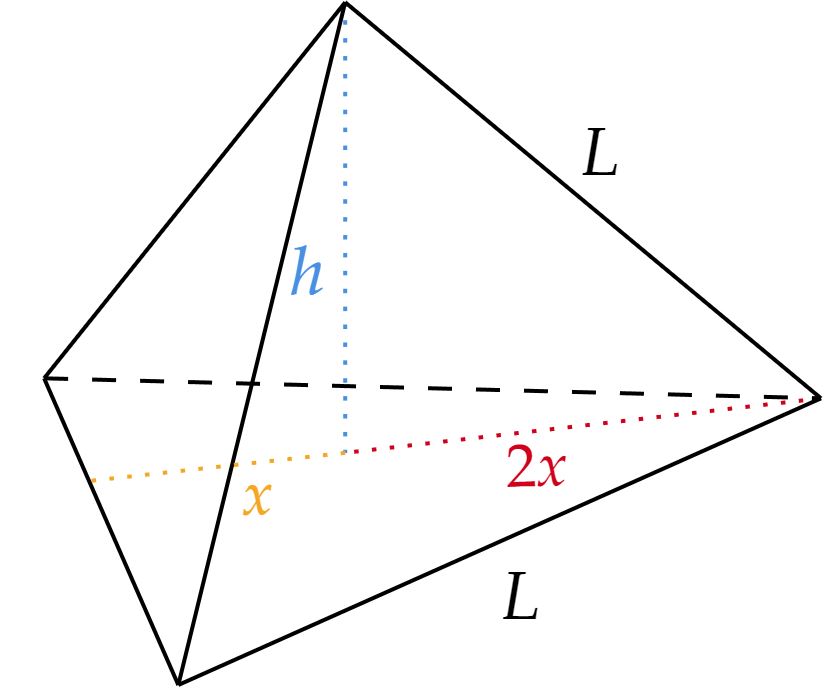\begin{matrix} 3x ={{\dfrac{L\sqrt{3}}{2} }}&\therefore& 2x = {{\dfrac{L\sqrt{3}}{3} }} \end{matrix}Continuando, agora é possível encontrar a altura do tetraedro utilizando Pitágoras, seja essa altura igual a $h$, então:\begin{matrix} L^2 = h^2 + (2x)^2 &\therefore& h= {{\dfrac{ L\sqrt{6}}{3}}} \end{matrix}Portanto, substituindo $L$ por $2\sqrt{2}$, o volume do tetraedro será:\begin{matrix} V = {{\dfrac{h}{3}}}\cdot {{ \left(\dfrac{L^2\sqrt{3}}{4}\right)}} && V = {{\dfrac{8}{3}}} \ u.v & \tiny{\blacksquare} \end{matrix}\begin{matrix}Letra \ (A) \end{matrix}