A princípio, vale lembrar que todo triângulo retângulo é inscritível, assim, a mediana relativa à hipotenusa é igual ao raio da circunferência circunscrita, ou seja, metade da hipotenusa. Nesse sentido, vamos esboçar a situação: 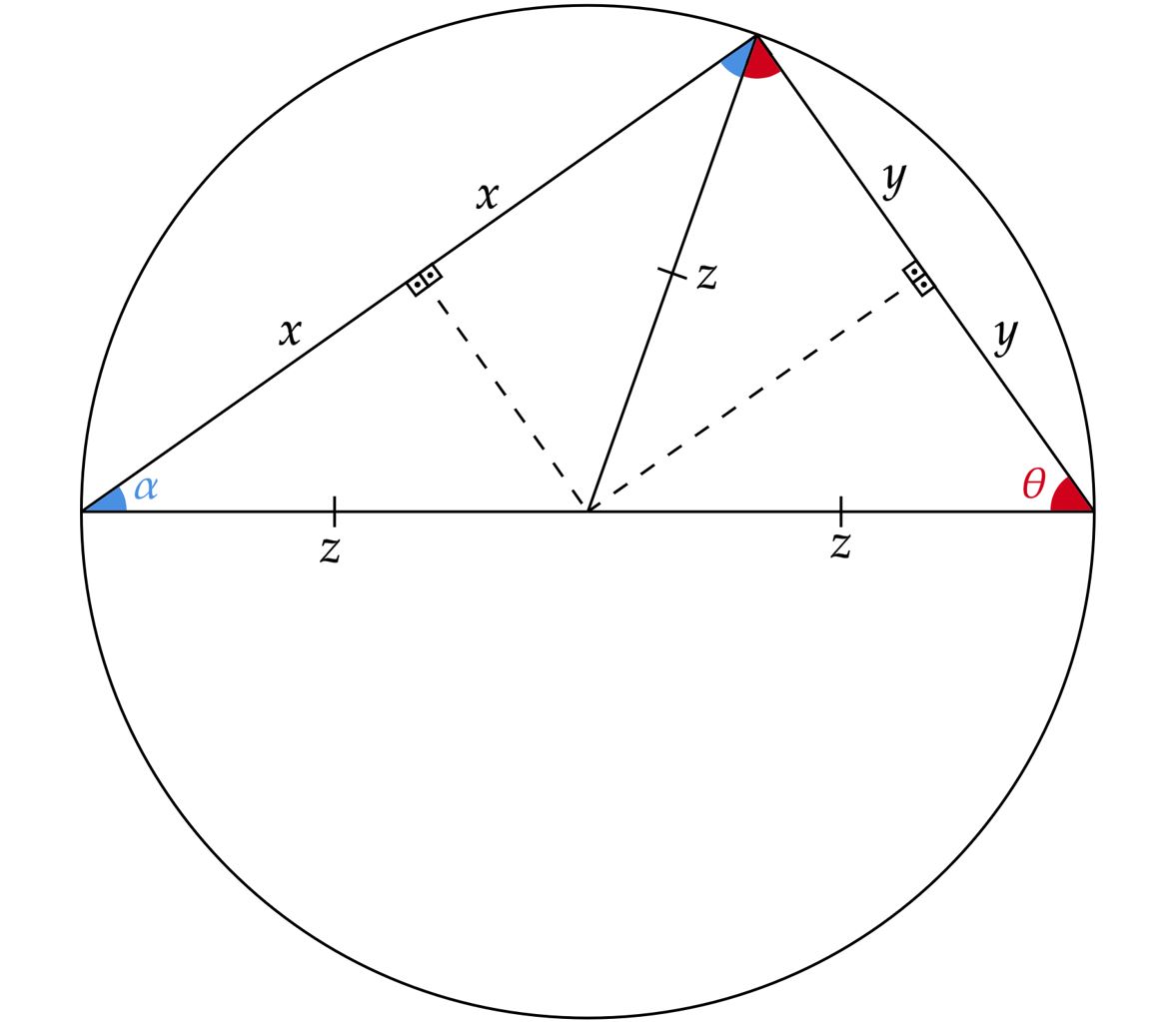Observe que há dois triângulos isósceles, assim, a partir do teorema de Pitágoras, pode-se escrever:\begin{matrix}z^2 = x^2 + y^2 & \text{(I)} \end{matrix}Conforme enunciado, têm-se:\begin{matrix} z = \sqrt{(2x)(2y)} = 2 \sqrt{xy}&\overset{ \text{(I)}}{\Rightarrow}&4xy =x^2 + y^2 \end{matrix}Resolvendo a equação de segundo grau em $x$:\begin{matrix} \underbrace{x^2 - 4xy + y^2 = 0}_{\Delta \ = \ 12y^2} &\Rightarrow& x = \dfrac{4y \pm 2y\sqrt{3}}{2} &\therefore&\dfrac{x}{y} = 2 + \sqrt{3} \end{matrix}Com isso, pensando no valor do cosseno dos ângulos, temos, respectivamente:\begin{matrix} \cos{\alpha} = \dfrac{x}{2 \sqrt{xy}} \color{#3368b8}{\cdot \dfrac{\sqrt{x}}{\sqrt{x}}}&,& \cos{\theta} = \dfrac{y}{2 \sqrt{xy}} \color{#3368b8}{\cdot \dfrac{\sqrt{y}}{\sqrt{y}}} \\ \\ \cos{\alpha} = \dfrac{1}{2} \sqrt{\dfrac{x}{y}} && \cos{\theta} = \dfrac{1}{2} \sqrt{\dfrac{y}{x}} \\ \\ \cos{\alpha} = \dfrac{ \sqrt{2 + \sqrt{3}}}{2} && \cos{\theta} = \dfrac{ 1}{2(2 - \sqrt{3})} \end{matrix}\begin{matrix}Letra \ (C) \end{matrix}