A maior dificuldade da questão é o entendimento da situação, veja a figura abaixo: 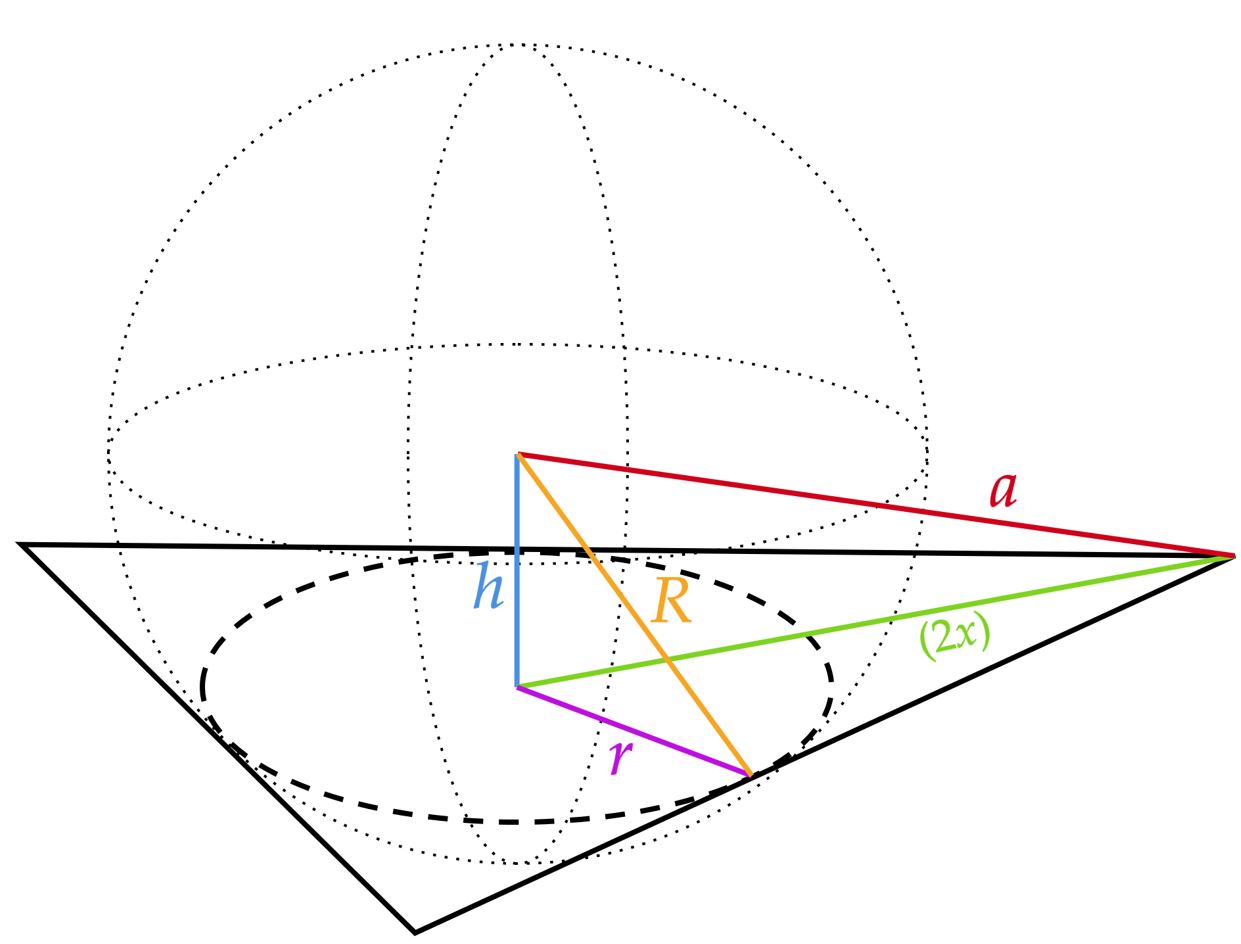Veja que, $r$ é o inraio, $R$ é o raio da esfera, $h$ é a distância do centro da esfera ao centro do círculo, enquanto $(2x)$ é a distância do vértice ao baricentro do triângulo, e por fim, $x$ que é a distância que queremos. Nessa perspectiva, vamos começar encontrando o inraio, veja a figura abaixo, não é difícil perceber que: 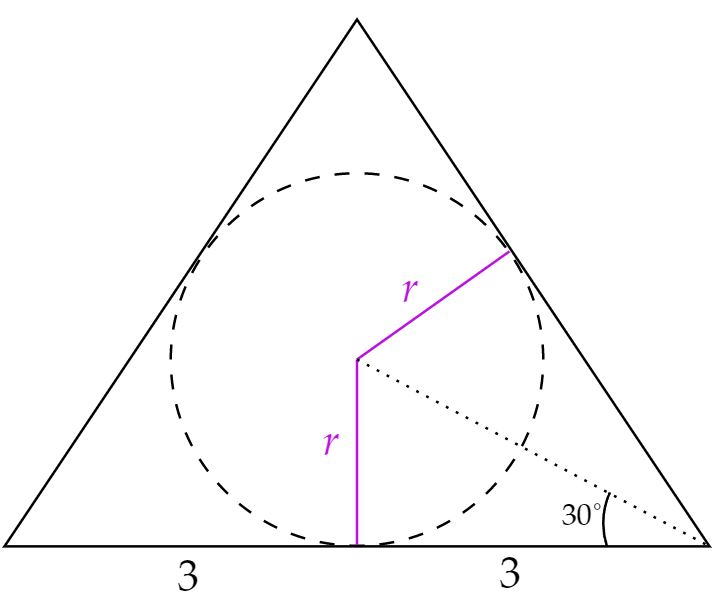\begin{matrix} \tan{30^{\circ}} = {{\dfrac{r}{3}}} &\therefore& r = \sqrt{3} \ \pu{cm} \end{matrix}Aplicando Pitágoras:\begin{matrix}4^2 = h^2 + r^2 &\therefore& h = \sqrt{13} \ \pu{cm} \end{matrix}Agora, precisamos encontrar $2x$, sendo a altura do triângulo equilátero $3x$, têm-se: \begin{matrix} 3x = {{\dfrac{6\sqrt{3}}{2}}} &\therefore& 2x = 2\sqrt{3} \ \pu{cm} \end{matrix}Novamente, aplicando Pitágoras: \begin{matrix} a^2 = (2x)^2 + h^2 &\therefore& a = 5 \ \pu{cm} & \tiny{\blacksquare} \end{matrix}\begin{matrix} Letra \ (C) \end{matrix}