A princípio, vamos esboçar a situação: 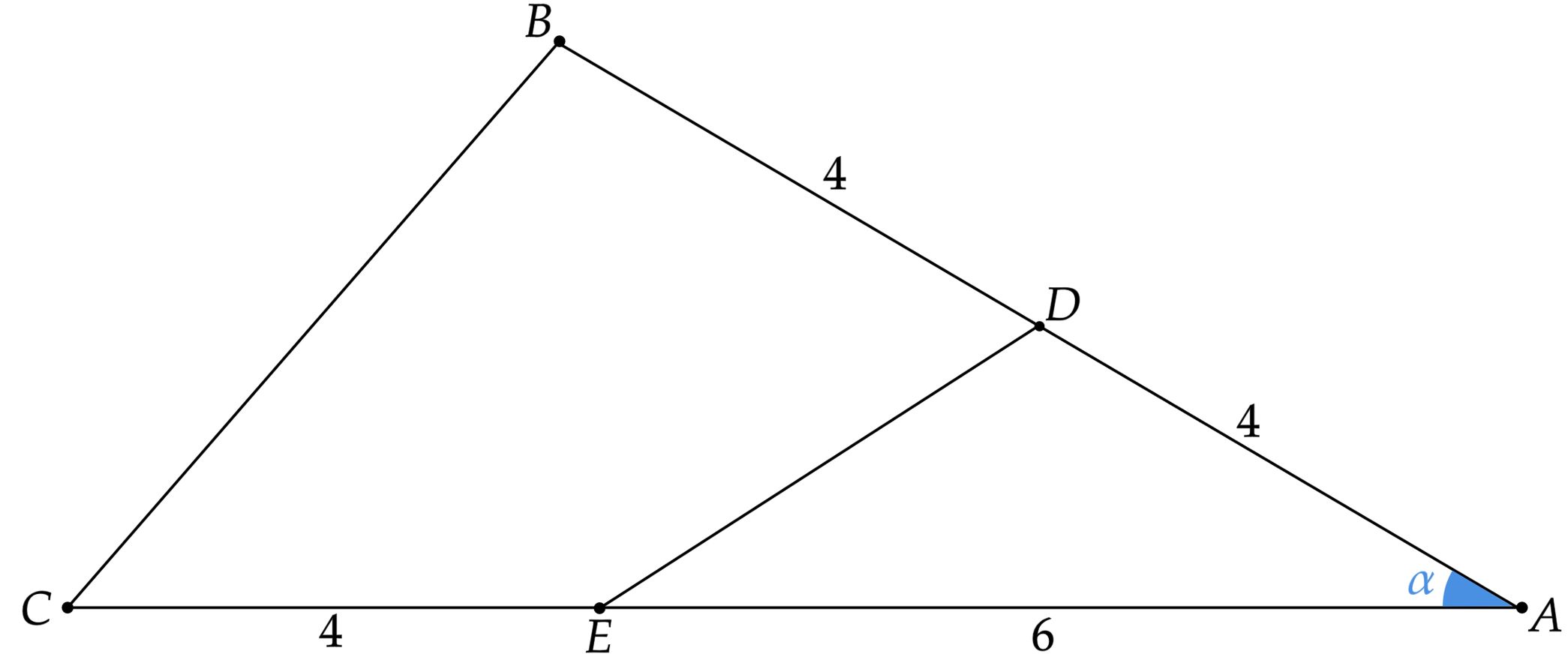Pensando na área dos triângulos, podemos escrever:\begin{matrix} \text{[ADE]} = \dfrac{(4) \cdot (6) \cdot \sin{\alpha}}{2} &,& \text{[ABC]} = \dfrac{(8) \cdot (10) \cdot \sin{\alpha}}{2} \end{matrix}Portanto,\begin{matrix} \dfrac{\text{[ADE]} }{\text{[ABC]} } = \dfrac{ \dfrac{(4) \cdot (6) \cdot \sin{\alpha}}{2} }{\dfrac{(8) \cdot (10) \cdot \sin{\alpha}}{2} } = \dfrac{3}{10} \end{matrix}\begin{matrix}Letra \ (D) \end{matrix}$\color{orangered}{\text{Obs:}}$ O triângulo em questão é pitagórico, ou seja, apresenta razão $3:4:5$ acerca de seus lados. Você pode verificar isso ao aplicar Pitágoras, mas também é intuitivo tentar escrever: $2(x):2(4):2(5)$.