A priori, sabemos que a circunferência maior está centrada em $C: (0,0)$, assim, podemos escrever sua equação como: $x^2 + y^2 = R^2$ , em que $R$ obviamente é o raio. Dessa forma, com conhecimento do ponto de tangência, não é difícil encontrar o raio, seja por $\text{Distância Euclidiana}$ ou por $\text{Pitágoras}$, veja: \begin{matrix} R^2 = 3^2 + 4^2 &\therefore& |R| = 5 \end{matrix}Continuando, pelo mesmo ponto de tangência ainda é possível encontrar a equação da reta: \begin{matrix}x_P.x + y_P.y= 5^2 &\therefore& 3x + 4y = 25 \end{matrix}$\color{orangered}{Obs:}$ Você também poderia encontrar pelo coeficiente angular da reta. Segundo enunciado, a circunferência menor possui centro sobre o eixo das abcissas, com isso, denotemos esse centro de $C^{'}: (a,0)$, atente que, ambas as circunferências são tangentes, por isso, seu raio $r$ será $r = |a-5|$. Nessa perspectiva, é válido esboçar a situação, pois faremos uma semelhança de triângulos, repare: 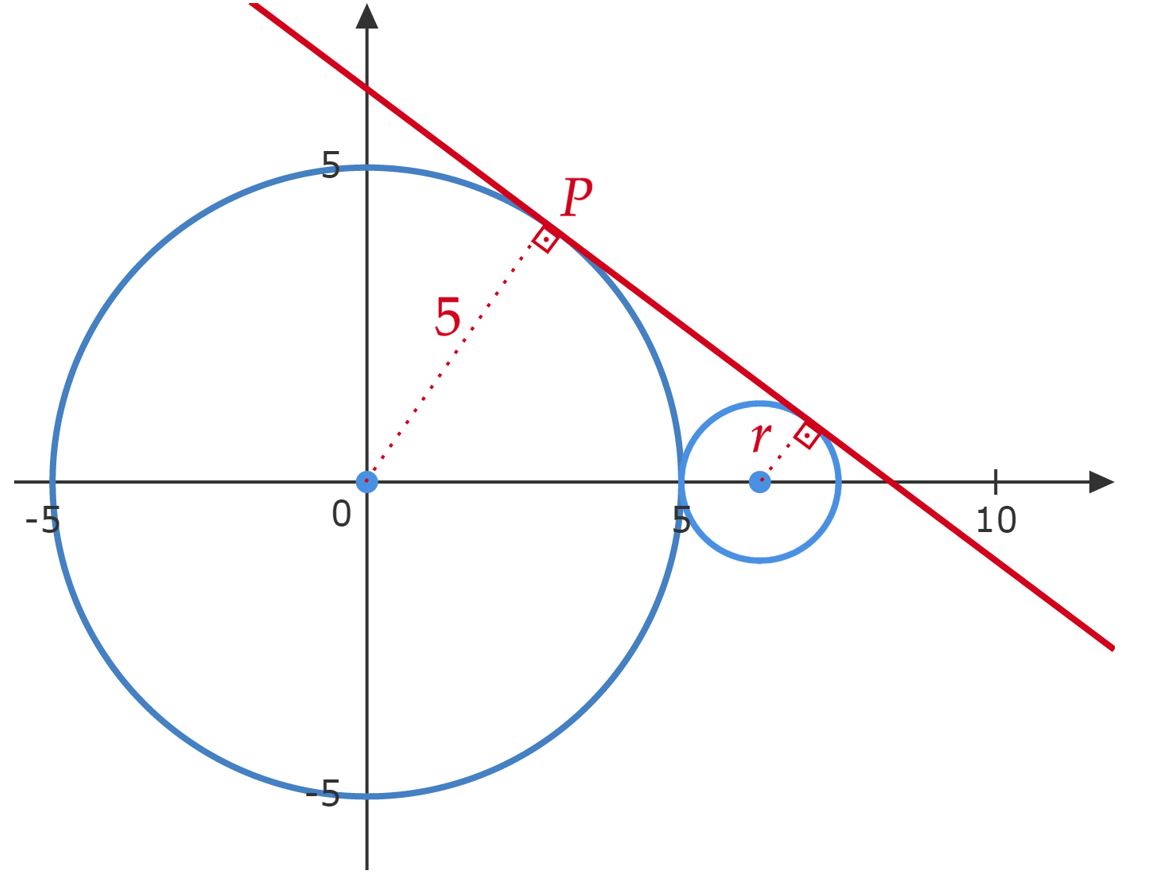$-$ Perceba os dois triângulos retângulos, a hipotenusa do triângulo maior será a distância da origem ao ponto de intersecção da reta com o eixo das abcissas, fazendo $y=0$ na equação da reta, têm-se a distância $x = \frac{25}{3}$. Enfim, a semelhança entre os catetos e hipotenusas: \begin{matrix} {\dfrac{5}{ \left(\dfrac{25}{3}\right) }} &=& { \dfrac{a-5}{\left(\dfrac{25}{3} - a\right)}} &\Rightarrow& \fbox{$a = {\dfrac{25}{4}}$} \end{matrix}Por fim, a equação da circunferência será: \begin{matrix} \pi: \left(x- \dfrac{25}{4}\right)^2 + y^2 =\dfrac{25}{16} \end{matrix}