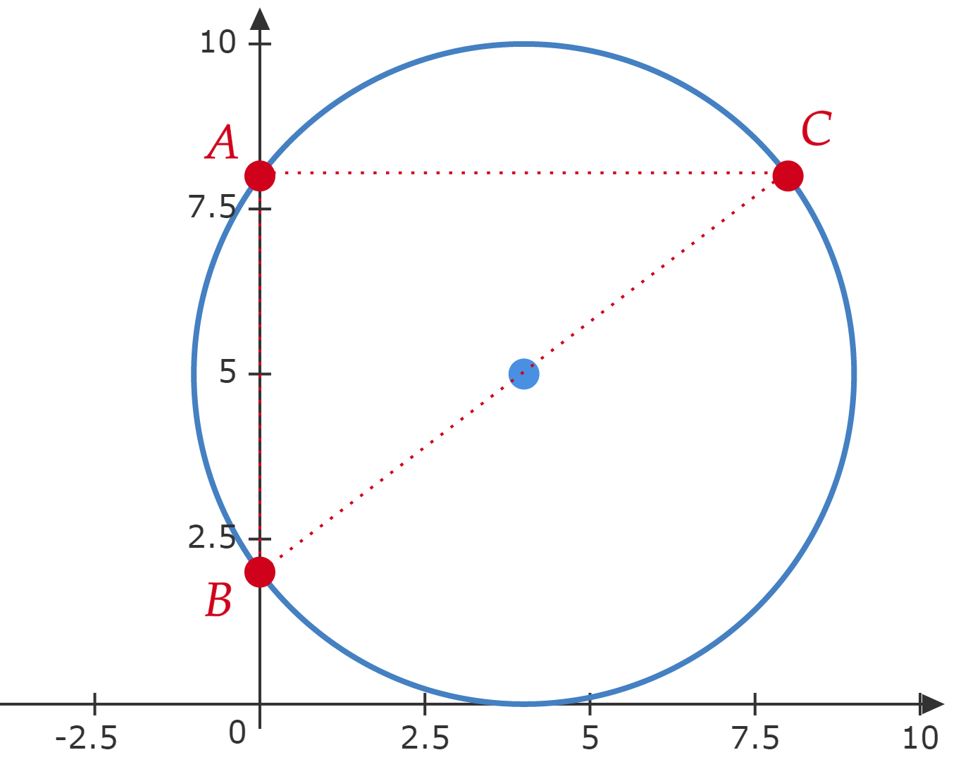
Uma circunferência passa pelos pontos , e . Então, o centro da circunferência e o valor de seu raio, respectivamente, são
CossenoGPT
Teste
gratuitamente agora
mesmo! 

$• \ \text{Resolução I:}$ Num raciocínio simples, atente que $\overline{AD} = \overline{BD}= \overline{CD} = R$ , em que $D$ é o centro da circunferência, localizado em $D:(x,y)$, e $R$ obviamente o raio. Nesse perspectiva, aplicando a $\text{Distância Euclidiana}$ temos o sistema de equações:\begin{matrix} \begin{cases} (x-0)^2 &+& (y-2)^2 &= &R^2 \\ (x-0)^2 &+& (y-8)^2 &= & R^2 \\ (x-8)^2 &+& (y-8)^2 &= & R^2
\end{cases} &\therefore& x= 4 &,& y = 5 &,& R= 5
\end{matrix}
$• \ \text{Resolução II:}$ Perceba que $B$ é perpendicular a $C$, sendo assim $\overline{AC}$ igual ao diâmetro da circunferência, aplicando Pitágoras no triângulo $ABC$, têm-se: \begin{matrix} (\overline{AC})^2 = 6^2 + 8^2 &\Rightarrow& \overline{AC} = 10 &\therefore& R =5
\end{matrix}
O centro da circunferência está no meio do segmento $\overline{AC}$ , logo: \begin{matrix} D: \left(\dfrac{x_A + x_C}{2} \ , \ \dfrac{y_A + y_C}{2}\right) &\therefore& D: (4 \ , \ 5)
\end{matrix}

Ampliar Imagem

