O gráfico ao lado mostra a variação, com o tempo, da velocidade de troca de calor durante uma reação química. Admita que de produto tenha se formado desde o início da reação até o tempo . Utilizando as informações contidas no gráfico, determine, de forma aproximada, o valor das quantidades abaixo, mostrando os cálculos realizados.
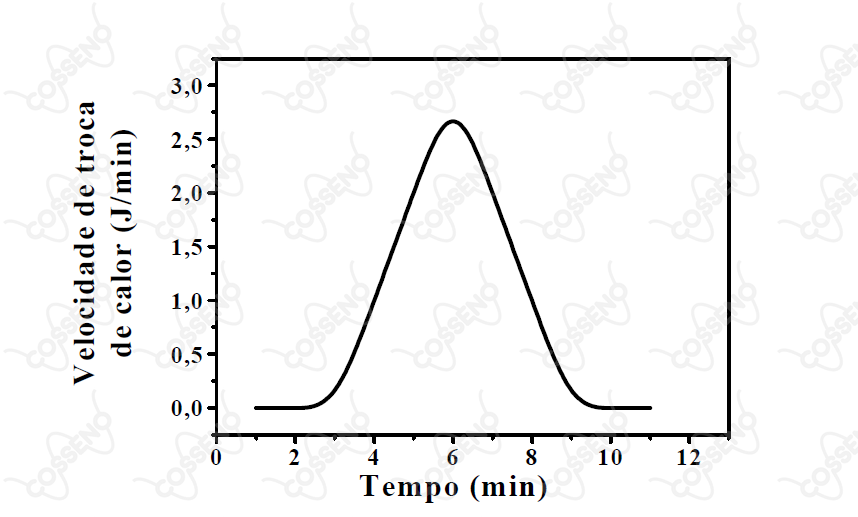
a) Quantidade, em mols, de produto formado até .
b) Quantidade de calor, em , liberada na reação até .
CossenoGPT
Teste
gratuitamente agora
mesmo! 

$-$ Como a questão informa que aceita valores aproximados, analisando o gráfico, pode-se perceber que a curva se assemelha muito a um triângulo, em que a área desse triângulo fornece a quantidade de calor utilizada na reação.
$• \ \text{a)}$ A quantidade de calor total da reação: \begin{matrix} Q_T \overset{N}{\approx} {\large{\frac{(9-3). (2,75 - 0)}{2}}} &\therefore& Q_T \approx 8,25 \ J
\end{matrix}Este é o calor necessário para produção de um mol de produto. Com isso, necessita-se saber quanto calor foi transferido no intervalo de quatro minutos, perceba que temos outro triângulo, este no caso, é retângulo: \begin{matrix} Q_{4 \ min}\overset{N}{\approx} {\large{\frac{(4-3). (1 - 0)}{2}}} &\therefore& Q_{4 \ min} \approx 0,5 \ J \end{matrix}Utilizando o fator unitário de conversão para encontrar o número de mols formado: \begin{matrix} n \approx {\large{\frac{1 \ mol}{8,25 \ J}}} \cdot 0,5 \ J &\therefore& n \approx 0,06 \ mol & \tiny{\blacksquare}
\end{matrix}
$• \ \text{b)}$ Pela alternativa $(a)$ já temos conhecimento deste resultado, basta "transformar" $J$ para $kJ$, veja: \begin{matrix} Q_T \approx 8,25 \ J \cdot {\large{\frac{kJ}{1000 \ J} }} &\therefore& Q \approx 8,25 \times 10^{-3} \ kJ & \tiny{\blacksquare}
\end{matrix}
$\color{orangered}{Obs:}$ Estamos admitindo que a troca de calor é proporcional a formação de produto.

