O circuito elétrico mostrado na figura é constituído por dois geradores ideais, com de força eletromotriz, cada um; dois capacitores de capacitâncias iguais a ; duas chaves e e sete resistores, cujas resistências estão indicadas na figura.
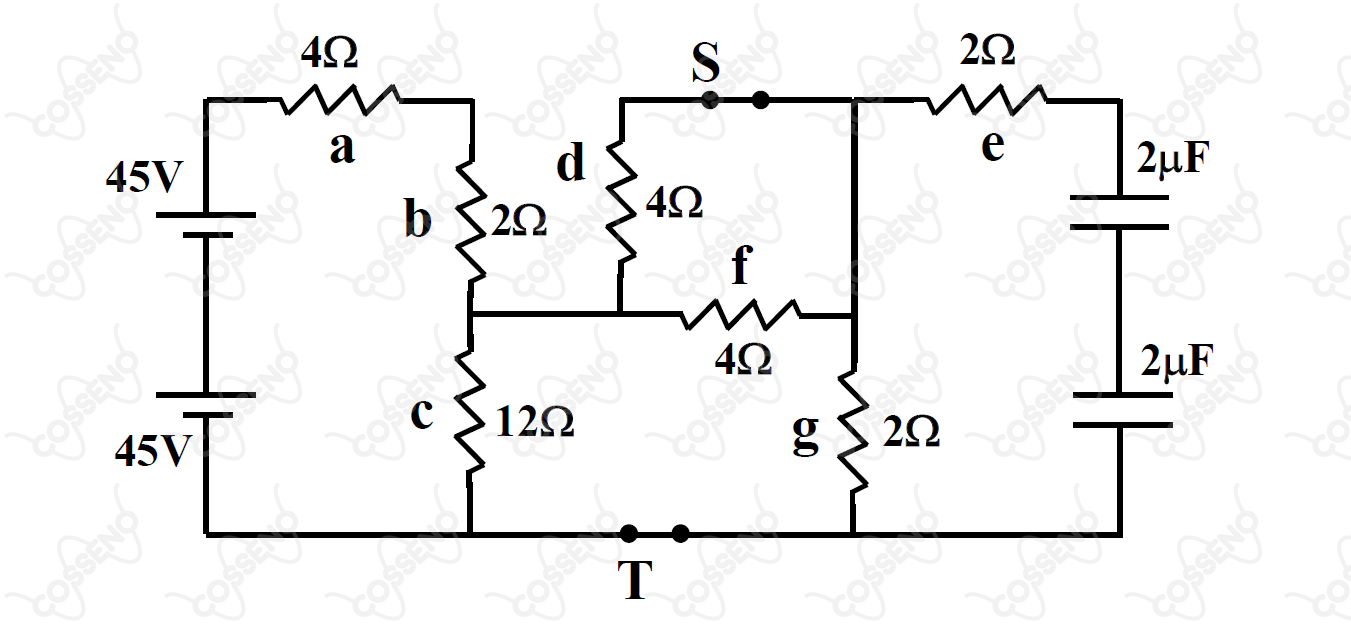
Considere que as chaves e se encontram inicialmente fechadas e que o circuito está no regime estacionário.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Vamos analisar o circuito com S e T fechados. Nesse caso, em regime estacionário, os capacitores se comportam como circuito aberto (não passa corrente). Assim, podemos encontrar a resistência equivalente simplificando o circuito:
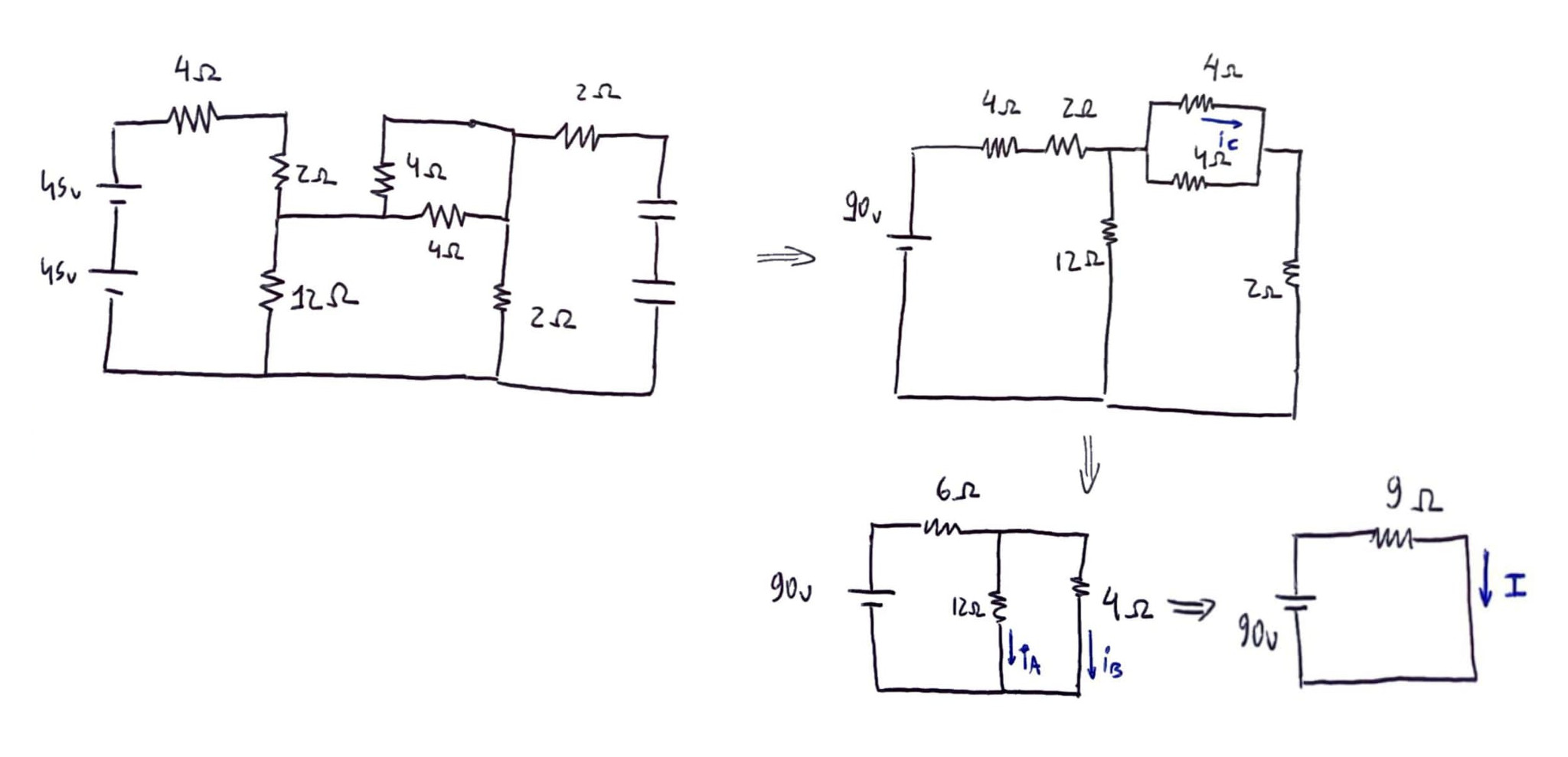 Acima foram indicadas correntes elétricas relevantes para a resolução.
Podemos então afirmar que $$I = \dfrac{\pu{90 V}}{\pu{9 \Omega}} = \boxed{\pu{10 A}}$$
Assim, podemos calcular $i_A$ e $i_B$ sabendo que:
$$\begin{cases}i_A + i_B = \pu{10 A}\quad\text{Lei dos nós}\\ i_A\cdot 12 = i_B\cdot 4\quad\text{Mesma queda de tensão}\end{cases}$$
Resolvendo o sistema de equações: $$\begin{cases}i_A = \pu{2,5 A} \\ i_B = \pu{7,5 A} \end{cases}$$
Note ainda que a corrente $i_B$ se divide em dois no paralelo $4\parallel 4$, de modo que $i_C = i_B/2 = \pu{3,75 A}$
Enfim, vamos julgar as alternativas.
---
a) Falso. Provamos acima que a corrente através de $d$ é igual a $i_C = \pu{3,75 A}$.
b) Falso. A diferença de potencial nos terminais do ramo em que os capacitores se encontram realmente é $2\ \Omega \cdot\pu{7,5 A} = \pu{15 V}$, mas como os capacitores estão em série, a ddp em cada um deles será igual a $15/2 = \pu{7,5 V}$.
c) Verdadeiro. Ao abrir a chave T, os capacitores (estando descarregados) se comportam como curto-circuito. É como se houvesse apenas a resistência de $2\ \Omega$ naquele ramo. Assim, a corrente $i_B$ será dividida em dois ramos de resistência $2\ \Omega$, cada uma de valor $i_B/2 = \pu{3,75 A}$.
d) Falso. Como provado no item anterior, a corrente é de $\pu{3,75 A}$.
e) Falso. Os capacitores associados em série terão capacitância igual a $$C = \dfrac{1}{\dfrac{1}{\pu{2 \mu F}}+\dfrac{1}{\pu{2 \mu F}}}=\pu{1 \mu F}$$Assim, quando os capacitores carregarem, a energia armazenada neles será de $$\epsilon = \dfrac{C\cdot U^2}{2} = \dfrac{1\cdot 10^{-6}\cdot 15^2}{2} = \pu{1,125 \cdot 10^{-4} J}$$
---
$$\boxed{\text{Gabarito C)}}$$
Acima foram indicadas correntes elétricas relevantes para a resolução.
Podemos então afirmar que $$I = \dfrac{\pu{90 V}}{\pu{9 \Omega}} = \boxed{\pu{10 A}}$$
Assim, podemos calcular $i_A$ e $i_B$ sabendo que:
$$\begin{cases}i_A + i_B = \pu{10 A}\quad\text{Lei dos nós}\\ i_A\cdot 12 = i_B\cdot 4\quad\text{Mesma queda de tensão}\end{cases}$$
Resolvendo o sistema de equações: $$\begin{cases}i_A = \pu{2,5 A} \\ i_B = \pu{7,5 A} \end{cases}$$
Note ainda que a corrente $i_B$ se divide em dois no paralelo $4\parallel 4$, de modo que $i_C = i_B/2 = \pu{3,75 A}$
Enfim, vamos julgar as alternativas.
---
a) Falso. Provamos acima que a corrente através de $d$ é igual a $i_C = \pu{3,75 A}$.
b) Falso. A diferença de potencial nos terminais do ramo em que os capacitores se encontram realmente é $2\ \Omega \cdot\pu{7,5 A} = \pu{15 V}$, mas como os capacitores estão em série, a ddp em cada um deles será igual a $15/2 = \pu{7,5 V}$.
c) Verdadeiro. Ao abrir a chave T, os capacitores (estando descarregados) se comportam como curto-circuito. É como se houvesse apenas a resistência de $2\ \Omega$ naquele ramo. Assim, a corrente $i_B$ será dividida em dois ramos de resistência $2\ \Omega$, cada uma de valor $i_B/2 = \pu{3,75 A}$.
d) Falso. Como provado no item anterior, a corrente é de $\pu{3,75 A}$.
e) Falso. Os capacitores associados em série terão capacitância igual a $$C = \dfrac{1}{\dfrac{1}{\pu{2 \mu F}}+\dfrac{1}{\pu{2 \mu F}}}=\pu{1 \mu F}$$Assim, quando os capacitores carregarem, a energia armazenada neles será de $$\epsilon = \dfrac{C\cdot U^2}{2} = \dfrac{1\cdot 10^{-6}\cdot 15^2}{2} = \pu{1,125 \cdot 10^{-4} J}$$
---
$$\boxed{\text{Gabarito C)}}$$

Ampliar Imagem

