A priori, denotemos as cargas de $q$, segundo enunciado, pode-se inferir que a onda irá deslocar as cargas verticalmente (estamos adotando um par de eixos coordenados). Nesse viés, comecemos pela energia potencial elétrica inicial, isto é, no instante $t=0$, em que têm-se: \begin{matrix} y (x,0) = {{(\dfrac{\pi}{2}})}\sin{x} \end{matrix}\begin{matrix} x= 0 &\therefore& y(0,0) = 0 &&,&&x = \pi &\therefore& y(\pi,0) = 0 \end{matrix}Deste modo, as cargas permanecem sobre o eixo vertical, distando-se o mesmo que inicialmente, ou seja, $\pi$. A partir desse resultado acima, encontra-se a energia inicial como: \begin{matrix} \fbox{$E_i = {{\dfrac{K|q^2|}{\pi}}}$} \end{matrix}O enunciado também fornece o período de onde, dele, têm-se: \begin{matrix} T = {{\dfrac{2\pi}{\omega}}} &\Rightarrow& T \cdot \omega = 2\pi \end{matrix}Com isso, analisando agora a energia final, iremos partir do instante $t =T/4$, logo: \begin{matrix} y \left(x,\dfrac{T}{4}\right) = -\left(\dfrac{\pi}{2}\right)\cos{x} \end{matrix}\begin{matrix} x= 0 &\therefore& y\left(0,\dfrac{T}{4}\right) = -{\left(\dfrac{\pi}{2}\right)} &&,&&x = \pi &\therefore& y\left(\pi,\dfrac{T}{4}\right) = {\left(\dfrac{\pi}{2}\right)} \end{matrix}A situação pode ser esboçada como: 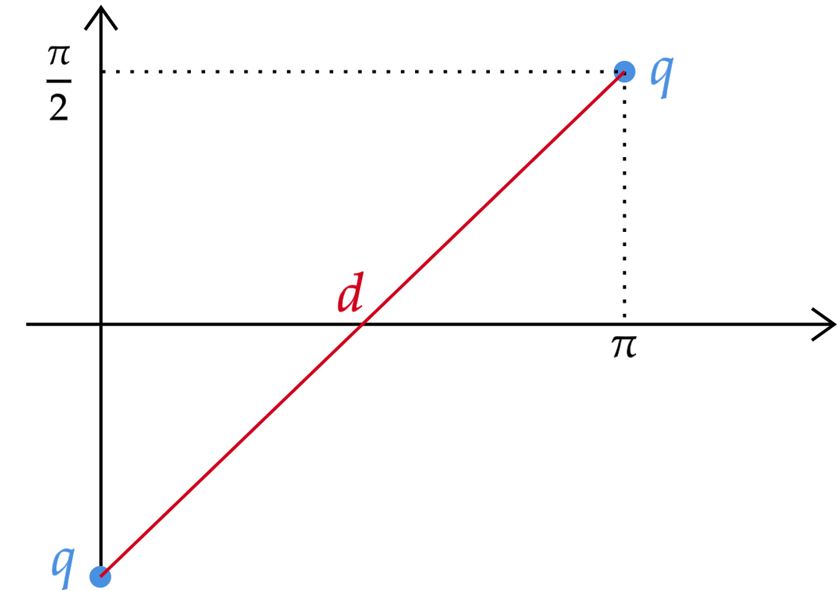É possível encontrar a distância $d$ de várias formas, e encontrando, você deve chegar no resultado: $d = \pi \sqrt{2}$ . Então, a energia final será: \begin{matrix} \fbox{$E_f = {{\dfrac{K|q^2|}{\pi \sqrt{2}}}}$} \end{matrix}Por fim, a razão solicitada: \begin{matrix} {{\dfrac{E_f}{E_i}}} = {{\dfrac{1}{\sqrt{2}}}} &\therefore& {{\dfrac{E_f}{E_i}}} = {{\dfrac{\sqrt{2}}{2}}} &\tiny{\blacksquare} \end{matrix}\begin{matrix} Letra \ (B) \end{matrix}