Na figura, e são fontes sonoras idênticas que emitem, em fase, ondas de freqüência e comprimento de onda . A distância entre as fontes é igual a .
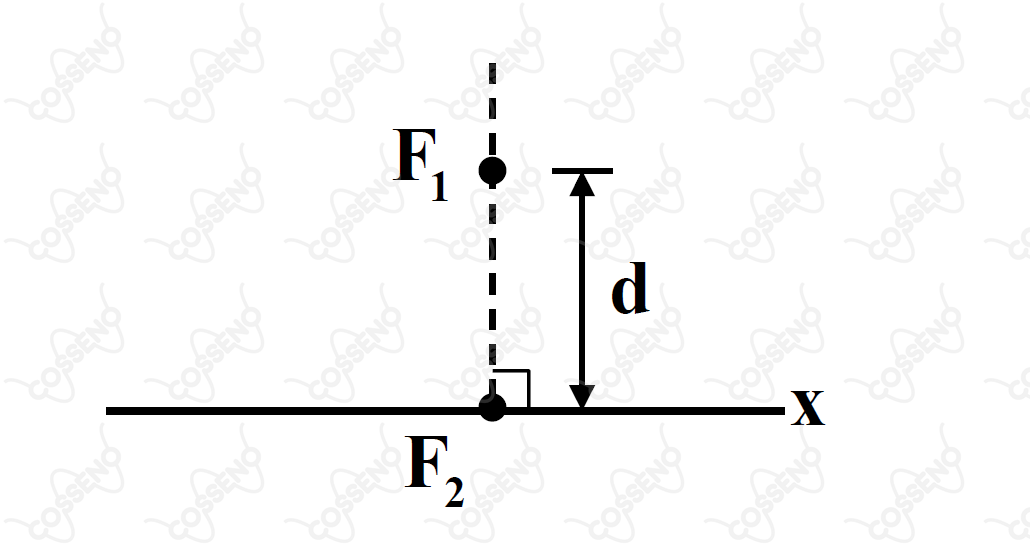
Pode-se então afirmar que a menor distância não nula, tomada a partir de , ao longo do eixo , para a qual ocorre interferência construtiva, é igual a
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A princípio, como a interferência deve ser construtiva, assim como as fontes estão em fase, tem-se para diferença de caminho óptico $\Delta x$:\begin{matrix}\Delta x = m \lambda &,& m \in \mathbb{N} &|& m = 0,1,2,3 \dots
\end{matrix}Assumindo que a distância tomada a partir de $F_2$ seja $x$, segue-se a geometria abaixo:
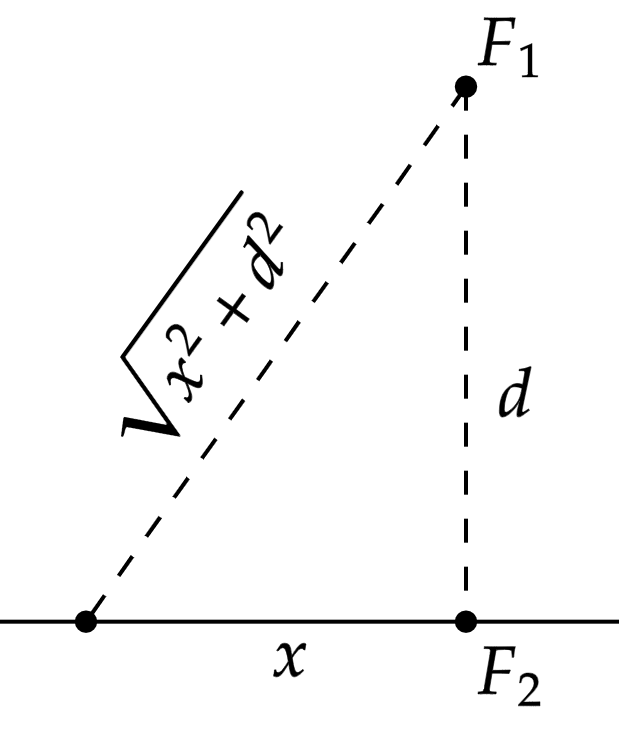 Ou seja,\begin{matrix}
\sqrt{x^2 + d^2} -x = m\lambda
\end{matrix}Continuando,\begin{matrix}
(\sqrt{x^2 + 9\lambda^2} )^2 =(x + m\lambda)^2
\end{matrix}Então,\begin{matrix}
x = \dfrac{\lambda(9-m^2)}{2m}
\end{matrix}Visto que o $x$ de interesse é o menor possível, deve-se avaliar qual valor de $m$ satisfaz essa condição, vejamos:\begin{matrix}
m = 0 &\longrightarrow& \text{(não convém)} \\
m = 1 &\longrightarrow& x = 4\lambda \\
m = 2 &\longrightarrow& \ \ \ \ x = 5\lambda/2 \\
m \ge 3 &\longrightarrow& \text{(não convém)}
\end{matrix}Portanto, $m$ deve ser igual a $2$, tal que:\begin{matrix}
x = \dfrac{5\lambda}{2} &\tiny{\blacksquare}
\end{matrix}\begin{matrix}Letra \ (B)
\end{matrix}
Ou seja,\begin{matrix}
\sqrt{x^2 + d^2} -x = m\lambda
\end{matrix}Continuando,\begin{matrix}
(\sqrt{x^2 + 9\lambda^2} )^2 =(x + m\lambda)^2
\end{matrix}Então,\begin{matrix}
x = \dfrac{\lambda(9-m^2)}{2m}
\end{matrix}Visto que o $x$ de interesse é o menor possível, deve-se avaliar qual valor de $m$ satisfaz essa condição, vejamos:\begin{matrix}
m = 0 &\longrightarrow& \text{(não convém)} \\
m = 1 &\longrightarrow& x = 4\lambda \\
m = 2 &\longrightarrow& \ \ \ \ x = 5\lambda/2 \\
m \ge 3 &\longrightarrow& \text{(não convém)}
\end{matrix}Portanto, $m$ deve ser igual a $2$, tal que:\begin{matrix}
x = \dfrac{5\lambda}{2} &\tiny{\blacksquare}
\end{matrix}\begin{matrix}Letra \ (B)
\end{matrix}

Ampliar Imagem

