A figura representa o percurso de um ciclista, num plano horizontal, composto de dois trechos retilíneos ( e ), cada um com de comprimento, e de um trecho sinuoso intermediário formado por arcos de circunferências de mesmo diâmetro, igual a , cujos centros se encontram numerados de a . Considere pontual o sistema ciclista–bicicleta e que o percurso é completado no menor tempo, com velocidade escalar constante.
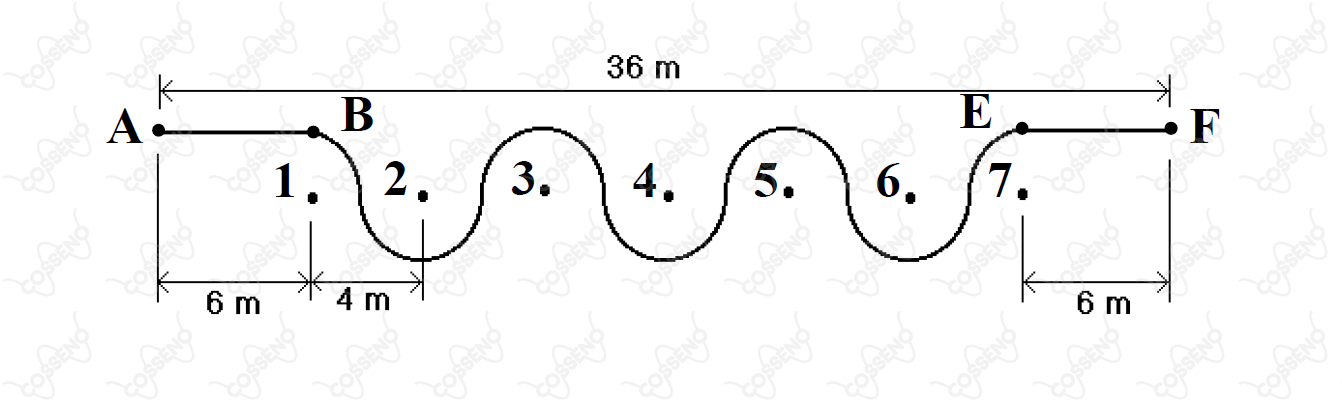
Se o coeficiente de atrito estático com o solo é , assinale a opção correta que indica, respectivamente, a velocidade do ciclista, o tempo despendido no percurso e a freqüência de zigue-zague no trecho .
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A princípio, atente que o percurso é num plano horizontal, assim, pensando nas curvas, podemos escrever:\begin{matrix}
F_{centrípeta} = F_{atríto}
\end{matrix}Nesse sentido, para maior velocidade - consequentemente menor tempo - o ciclista deve inclinar sua bicicleta a fim de atingir a maior força de atrito possível, esta que será quando:\begin{matrix}F_{atrito} = \mu N &,& N = mg
\end{matrix}Com isso,\begin{matrix}\dfrac{mv^2}{R} = \mu mg &\Rightarrow&v =\sqrt{\mu Rg}
\end{matrix}Como o diâmetro das curvas é $4,0 \ \pu{m}$, o raio $R$ deve ser $2,0 \ \pu{m}$, logo:\begin{matrix} v = \sqrt{0,8 \cdot 2,0 \cdot 10} &\therefore& \boxed{v =4,0 \ \pu{m/s}}
\end{matrix}Já para o tempo desprendido, precisamos encontrar a distância percorrida nos arcos de circunferência. Para isso, vamos começar observando que temos $12$ quartos de circunferência, além de mais dois trechos de $6 \ \pu{m}$ cada, ou seja, a distância total $d$ foi:\begin{matrix}
d = 2 \cdot 6 + \dfrac{12}{4}(2\pi R) &\therefore& d = 48 \ \pu{m} &,& \pi \approx 3
\end{matrix}Portanto, o tempo desprendido para realizar todo o percurso foi:\begin{matrix}\Delta t =\dfrac{48}{4} &\therefore& \boxed{\Delta t = 12 \ \pu{s}}
\end{matrix}Por fim, a frequência de zigue-zague:\begin{matrix}
\omega = 2\pi f &,& \omega = \dfrac{v}{R}
\end{matrix}Assim,\begin{matrix}2\pi f = \dfrac{v}{R} &\therefore& \boxed{f \approx 0,32 \ \pu{s^{-1}}}
\end{matrix}\begin{matrix}Letra \ (B)
\end{matrix}

