Um atleta mantém-se suspenso em equilíbrio, forçando as mãos contra duas paredes verticais, perpendiculares entre si, dispondo seu corpo simetricamente em relação ao canto e mantendo seus braços horizontalmente alinhados, como mostra a figura.
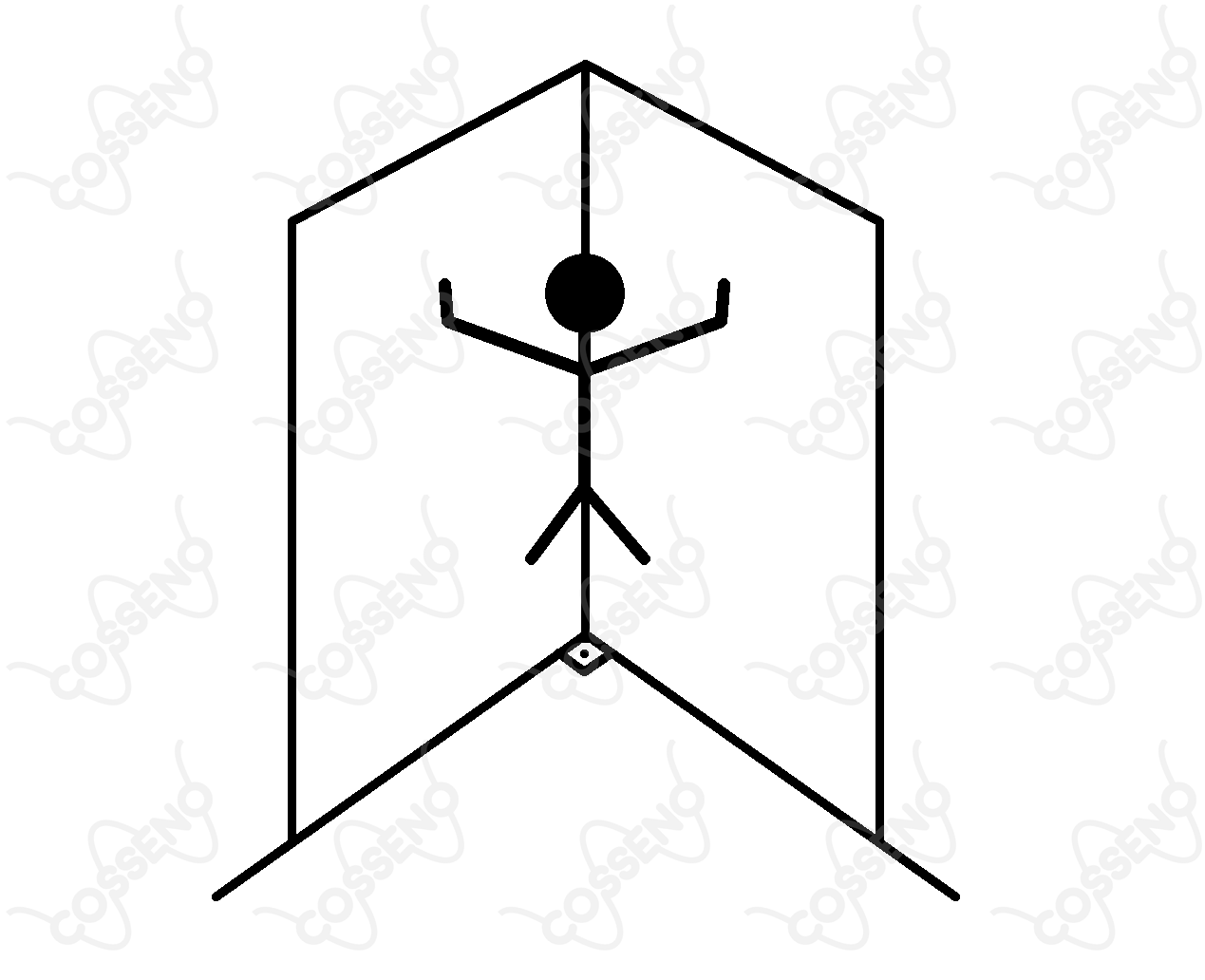
Sendo a massa do corpo do atleta e o coeficiente de atrito estático interveniente, assinale a opção correta que indica o módulo mínimo da força exercida pelo atleta em cada parede.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A grande dificuldade deste problema é sua geometria, pois não é nada trivial pensar nas forças em três dimensões. Veja na figura a seguir as primeiras forças que atuam no atleta.
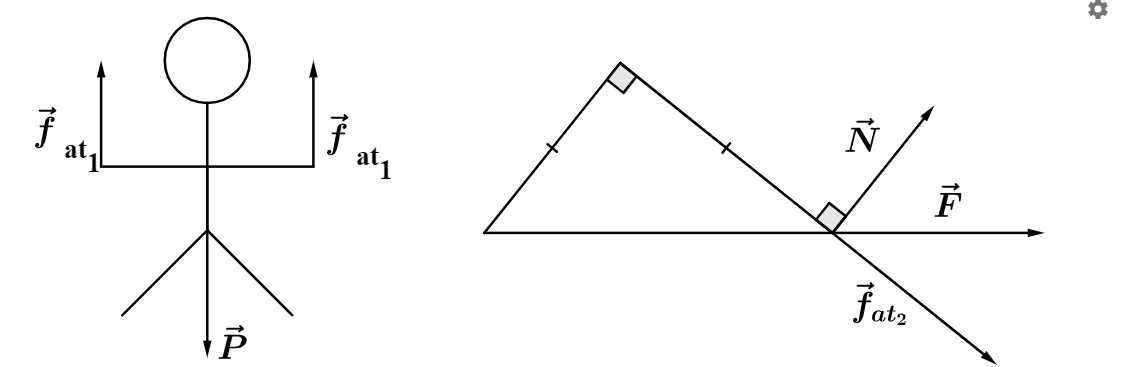 Na configuração da esquerda, temos
$$2\vert \vec{f}_{at_{1}} \vert = mg \Rightarrow \vert \vec{f}_{at_{1}} \vert = \dfrac{mg}{2}. \ (1)$$
No entanto, ainda falta a força que o atleta aplica na parede, veja a decomposição das forças em uma vista superior na configuração da direita na figura.
$$\vert \vec{N} \vert = \vert \vec{f}_{at_{2}} \vert. \ (2)$$
Além disso,
$$\vert \vec{f}_{at} \vert^{2} = \vert \vec{f}_{at_{1}} \vert^{2} + \vert \vec{f}_{at_{2}} \vert^{2}, \ (3)$$
corresponde a resultante da força de atrito que será utilizada na equação que depende de $N$. Portanto,
$$\sqrt{\vert \vec{f}_{at_{1}} \vert^{2} + \vert \vec{f}_{at_{2}} \vert^{2}} = \mu N \\
\vert \vec{f}_{at_{1}} \vert^{2} + \vert \vec{f}_{at_{2}} \vert^{2} = \mu^{2} N^{2} \\
\dfrac{m^{2}g^{2}}{4} = N^{2}(\mu^{2} - 1) \\
N = \dfrac{mg}{2} \cdot \dfrac{1}{\sqrt{\mu^{2} - 1}} \ (4)$$
O enunciado pede a força mínima exercida pelo atleta pela parede, logo tal força se traduz como a resultante de todas as forças que calculamos, uma força que atua fora do plano. Faça em seu caderno a decomposição das forças, sabendo que ambas as forças de atritos estão contidas no mesmo plano da parede e a normal está fora do plano. Fazendo isso, vamos obter
$$\vert \vec{F} \vert^{2} = \vert \vec{N} \vert^{2} + \vert \vec{f}_{at} \vert^{2}\\
\vert \vec{F} \vert = \dfrac{mg}{2} \cdot \left(\dfrac{\mu^{2} + 1}{\mu^{2} - 1}\right)^{\frac{1}{2}}$$
Na configuração da esquerda, temos
$$2\vert \vec{f}_{at_{1}} \vert = mg \Rightarrow \vert \vec{f}_{at_{1}} \vert = \dfrac{mg}{2}. \ (1)$$
No entanto, ainda falta a força que o atleta aplica na parede, veja a decomposição das forças em uma vista superior na configuração da direita na figura.
$$\vert \vec{N} \vert = \vert \vec{f}_{at_{2}} \vert. \ (2)$$
Além disso,
$$\vert \vec{f}_{at} \vert^{2} = \vert \vec{f}_{at_{1}} \vert^{2} + \vert \vec{f}_{at_{2}} \vert^{2}, \ (3)$$
corresponde a resultante da força de atrito que será utilizada na equação que depende de $N$. Portanto,
$$\sqrt{\vert \vec{f}_{at_{1}} \vert^{2} + \vert \vec{f}_{at_{2}} \vert^{2}} = \mu N \\
\vert \vec{f}_{at_{1}} \vert^{2} + \vert \vec{f}_{at_{2}} \vert^{2} = \mu^{2} N^{2} \\
\dfrac{m^{2}g^{2}}{4} = N^{2}(\mu^{2} - 1) \\
N = \dfrac{mg}{2} \cdot \dfrac{1}{\sqrt{\mu^{2} - 1}} \ (4)$$
O enunciado pede a força mínima exercida pelo atleta pela parede, logo tal força se traduz como a resultante de todas as forças que calculamos, uma força que atua fora do plano. Faça em seu caderno a decomposição das forças, sabendo que ambas as forças de atritos estão contidas no mesmo plano da parede e a normal está fora do plano. Fazendo isso, vamos obter
$$\vert \vec{F} \vert^{2} = \vert \vec{N} \vert^{2} + \vert \vec{f}_{at} \vert^{2}\\
\vert \vec{F} \vert = \dfrac{mg}{2} \cdot \left(\dfrac{\mu^{2} + 1}{\mu^{2} - 1}\right)^{\frac{1}{2}}$$

Ampliar Imagem

