A figura plana ao lado mostra os elementos de um circuito elétrico. Nesse mesmo plano encontram-se duas espiras interligadas, e , de comprimentos relativamente curtos em comparação aos dois fios condutores próximos ( e ).
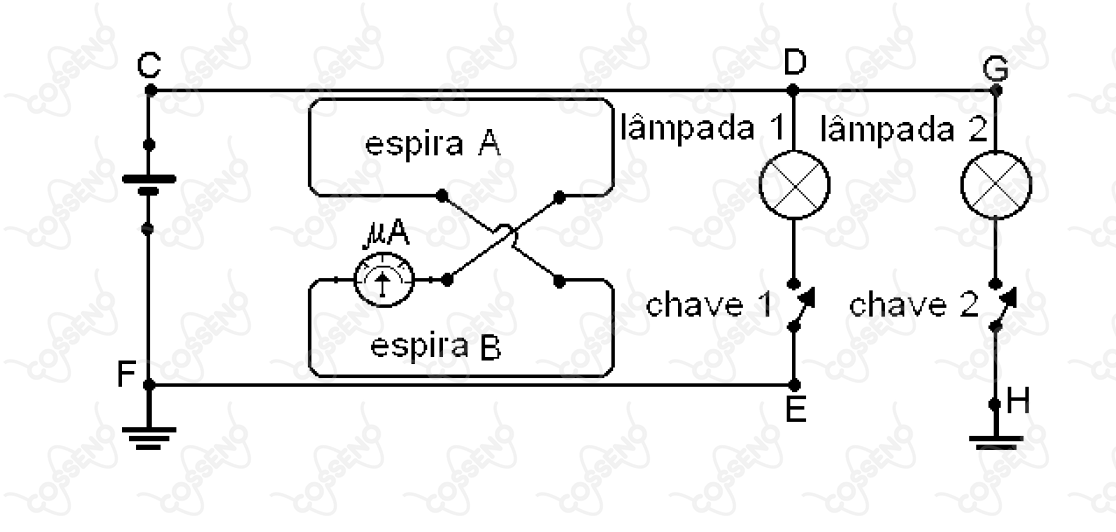
A deflexão do ponteiro do micro-amperímetro, intercalado na espira , só ocorre instantaneamente no momento em que
CossenoGPT
Teste
gratuitamente agora
mesmo! 

$• \ \text{Alternativas (A) e (B):}$ $\color{orangered}{\text{Incorretas}}$
Pensando na chave $1$, ao ligarmos teremos uma corrente de mesma intensidade, mas sentidos opostos entre os segmentos $\overline{CD}$ e $\overline{EF}$, assim como $\overline{CF}$ e $\overline{DE}$. No caso, o circuito irá produzir um campo magnético, consequentemente, pela Lei de Lenz, a espira irá produzir uma corrente induzida a fim de reprimir este efeito, produzindo outro campo contrário. Contudo, o ponteiro deve permanecer o mesmo, pois a corrente produzida em $B$ é contrária à de $A$ (simetria), assim elas se anularão, visto que apresentarão a mesma intensidade - idealmente falando.
$• \ \text{Alternativas (C), (D) e (E):}$ $\color{#3368b8}{\text{Apenas uma é correta}}$
Ao ligar a chave $2$ a corrente irá seguir um único trajeto direto; $CDGH$, ou seja, não haverá a produção de um campo magnético análogo por $\overline{EF}$. Portanto, a espira deve produzir uma corrente que nesta situação não será completamente anulada, pois a intensidade do campo em $A$ e diferente de $B$. Além disso, o raciocínio é análogo ao desligar, veja que em determinado momento teremos um regime estacionário, com a espira apresentando uma corrente constante. Desligando-se a chave, o campo magnético produzido pelo circuito irá cessar, assim como a espira irá atenuar sua corrente até que não haja mais intensidade.\begin{matrix}Letra \ (D)
\end{matrix}$\color{orangered}{\text{Obs:}}$ Repare que o enunciado diz "só", o que impõe exclusividade. Nesse contexto, não são aceitáveis as repostas $(C)$ e $(E)$, visto que são apenas possibilidades, em que uma pode contradizer a exclusividade da outra.

