Em 1879, Edwin Hall mostrou que, numa lâmina metálica, os elétrons de condução podem ser desviados por um campo magnético, tal que no regime estacionário, há um acúmulo de elétrons numa das faces da lâmina, ocasionando uma diferença de potencial entre os pontos e , mostrados na figura.
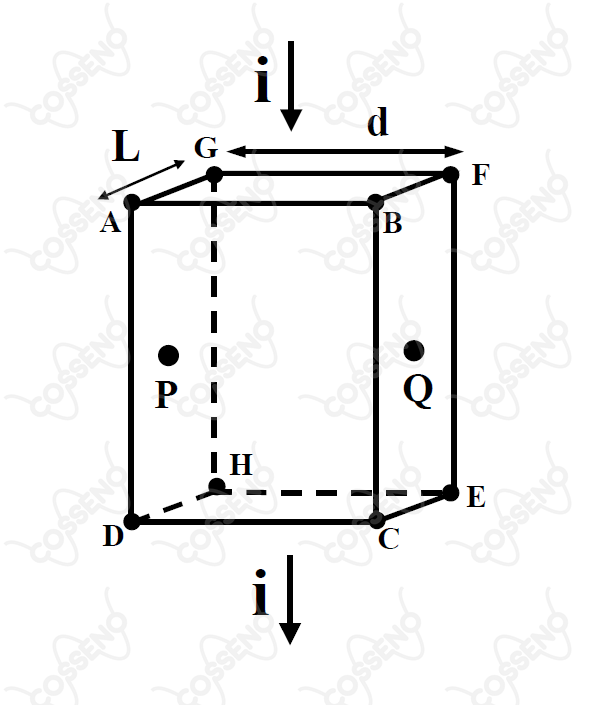
Considere, agora, uma lâmina de cobre de espessura e largura , que transporta uma corrente elétrica de intensidade , imersa no campo magnético uniforme que penetra perpendicularmente a face , no mesmo sentido de para . Assinale a alternativa correta.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

$• \ \text{Alternativa (A):}$ $\color{orangered}{\text{Incorreta}}$
A princípio, lembre-se que o sentido da corrente elétrica é convencionalmente oposto ao dos elétrons. Nesse sentido, os elétrons devem percorrer de $C$ para $B$, tal que pela regra da mão direita, deve surgir uma força magnética no sentido de $Q$ radial ao plano. Com isso, sabemos que terá acúmulo de carga negativa $q$ em $Q$, provoca-se assim a diferença de potencial $V_H$ e um campo elétrico de $P$ para $Q$. Desse modo, o acúmulo de carga deve crescer até o momento em que a força elétrica que atua no elétron seja equivalente a força magnética, isto é:\begin{matrix}F_{elétrica} = F_{magnética}
\end{matrix}Não se esqueça que $V_H = E \cdot d$, então:\begin{matrix}E \cdot q = B \cdot q \cdot V_e &\Rightarrow& V_e = \dfrac{V_H}{Bd}
\end{matrix}$• \ \text{Alternativa (B):}$ $\color{orangered}{\text{Incorreta}}$
Como dito anteriormente, o acúmulo de carga negativa será em $Q$, ou seja, o seu potencial será menor.
$• \ \text{Alternativa (C):}$ $\color{orangered}{\text{Incorreta}}$
Na verdade, eles se acumulam na face $BCEF$.
$• \ \text{Alternativa (D):}$ $\color{#3368b8}{\text{Correta}}$
Pondere o que foi discutido na alternativa $(A)$, ao imprimirmos uma velocidade idêntica a dos elétrons no sentido oposto, estes estarão em repouso relativo ao campo magnético. Com isso, não deve haver força magnética, prevalecendo a força elétrica, esta que irá redistribuir a sobrecarga das faces, ou seja, irá se acumular elétrons em $P$ até o ponto de equilibrar o potencial entre $Q$ e $P$.
$• \ \text{Alternativa (E):}$ $\color{orangered}{\text{Incorreta}}$
A $(D)$ está correta.\begin{matrix}Letra \ (D)
\end{matrix}

16:50 06/09/2024
Não consegui entender o porquê da velocidade relativa ser nula. Se a velocidade for aplicada à lâmpada, ela estará indo no sentindo de B para C, enquanto os elétrons, de C para B graças ao sentido da corrente. Assim, a velocidade relativa não seria nula. Qual o erro desse raciocínio?

