Tubos de imagem de televisão possuem bobinas magnéticas defletoras que desviam elétrons para obter pontos luminosos na tela e, assim, produzir imagens. Nesses dispositivos, elétrons são inicialmente acelerados por uma diferença de potencial entre o catodo e o anodo. Suponha que os elétrons são gerados em repouso sobre o catodo. Depois de acelerados, são direcionados, ao longo do eixo , por meio de uma fenda sobre o anodo, para uma região de comprimento onde atua um campo de indução magnética uniforme , que penetra perpendicularmente o plano do papel, conforme mostra o esquema. Suponha, ainda, que a tela delimita a região do campo de indução magnética.
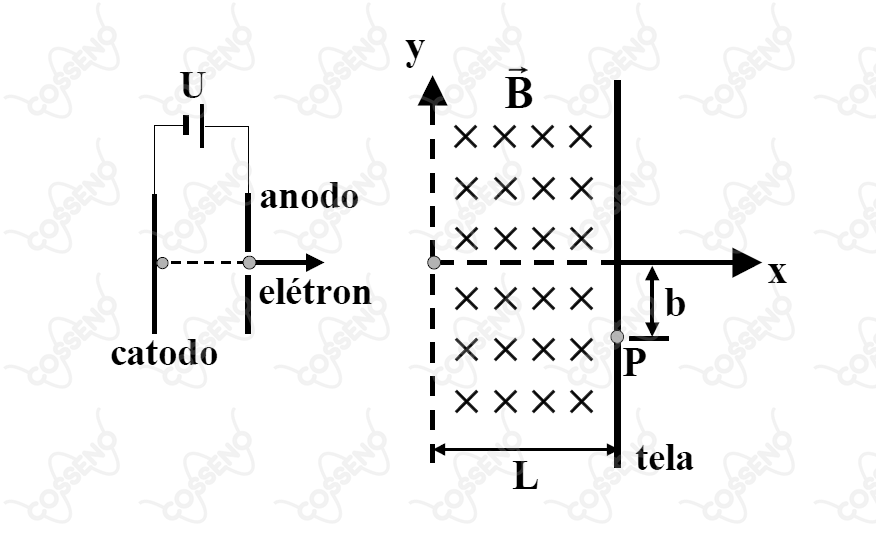
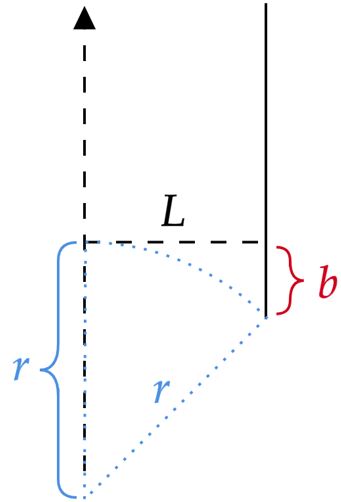
Se um ponto luminoso é detectado a uma distância sobre a tela, determine a expressão da intensidade de necessária para que os elétrons atinjam o ponto luminoso , em função dos parâmetros e constantes fundamentais intervenientes. (Considere ).
CossenoGPT

Ampliar Imagem

