Analisando o movimento do centro de massa, pode-se esboçar: 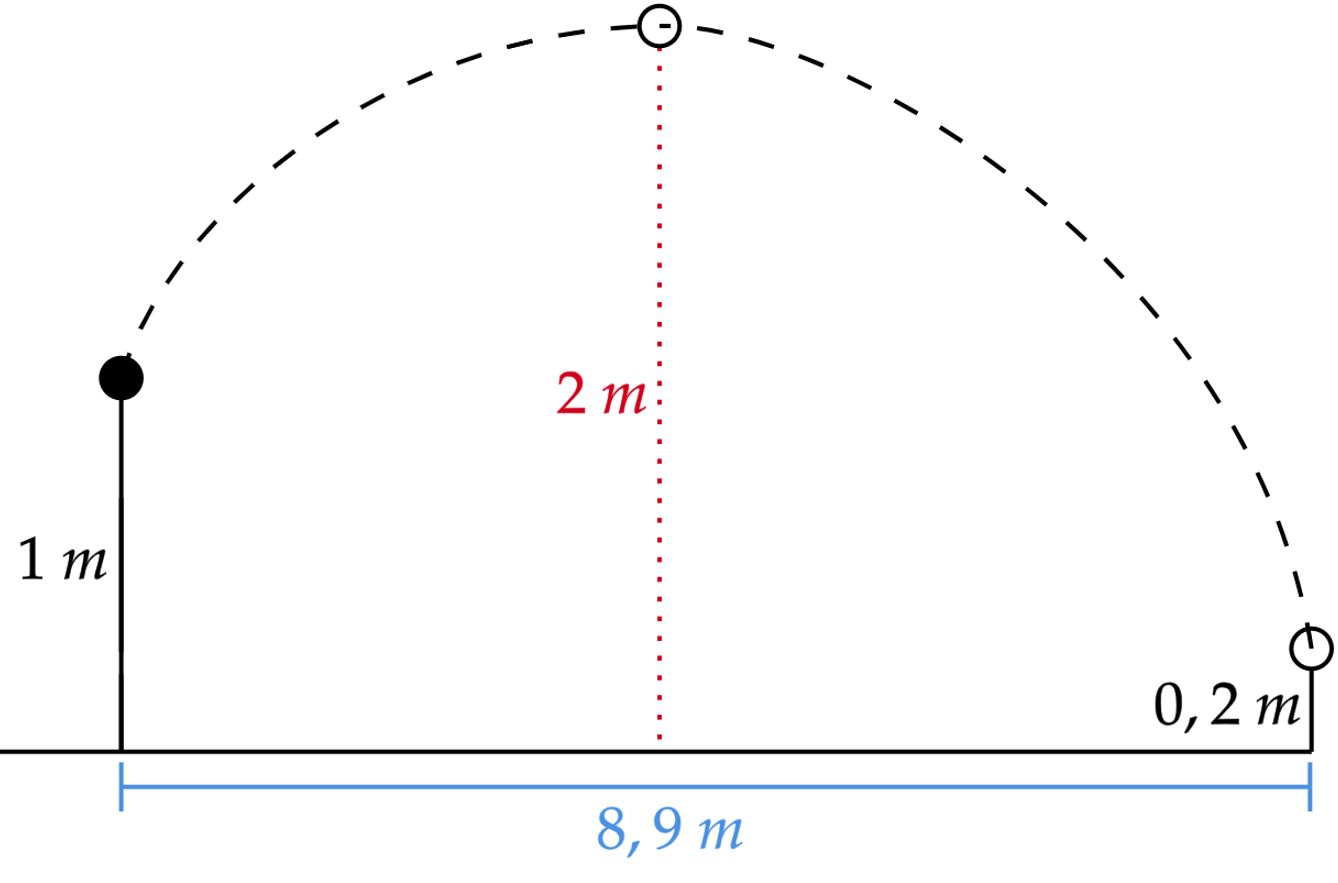A princípio, veja que o movimento na horizontal é retilíneo e uniforme, ou seja, a velocidade horizontal pode ser escrita como:\begin{matrix}v_x = \dfrac{8,9}{t_s + t_q} & (1) \end{matrix}Em que $t_s$ e $t_q$ são, respectivamente, os tempos de subida e queda do atleta. Nesse sentido, vamos começar pensando na subida, pela equação horária do movimento uniformemente variado na vertical, temos:\begin{matrix}\Delta y =V_y\cdot t_s- (-g)\dfrac{(t_s)^2}{2} \end{matrix}Na altura máxima a velocidade vertical deve ser nula, então,\begin{matrix}(2-1) = g\dfrac{(t_s)^2}{2} &\Rightarrow& t_s = \sqrt{\dfrac{2}{g}} \approx 0,45 \ \pu{s} \end{matrix}$\color{orangered}{\text{Obs:}}$ $g = 10 \ \pu{m/s^2}$ e $\sqrt{20} \approx 4,5$ Já para o tempo de queda, iremos admitir um raciocínio análogo:\begin{matrix}\Delta y =V_y\cdot t_q + (-g)\dfrac{(t_q)^2}{2} \end{matrix}Novamente, lembre-se que na altura máxima a velocidade vertical deve ser nula, então,\begin{matrix}(0,2-2) = g\dfrac{(t_q)^2}{2} &\Rightarrow& t_s = \sqrt{\dfrac{3,6}{g}} = 0,60 \ \pu{s} \end{matrix}Desse modo, substituindo nossos resultados em $(1)$:\begin{matrix} v_x = \dfrac{8,9}{0,45+ 0,60} \approx 8,5 \ \pu{m/s} \end{matrix}\begin{matrix}Letra \ (A) \end{matrix}