Num experimento de duas fendas de Young, com luz monocromática de comprimento de onda , coloca-se uma lâmina delgada de vidro sobre uma das fendas. Isto produz um deslocamento das franjas na figura de interferência.
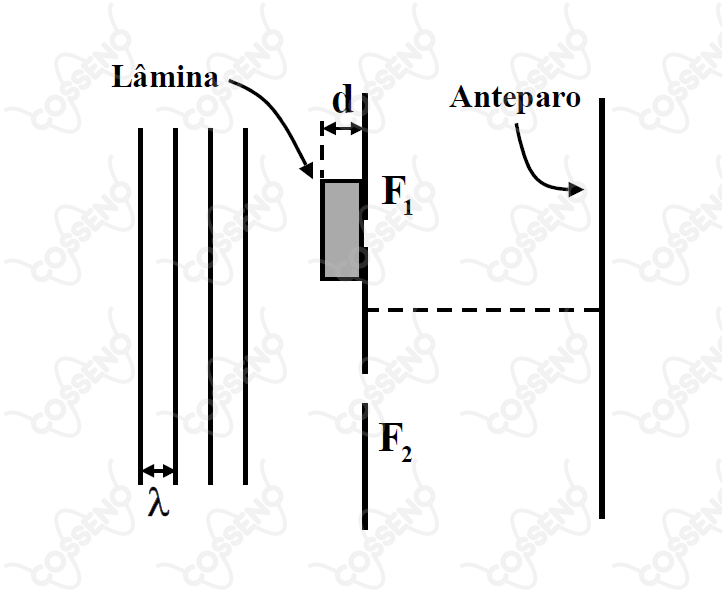
Considere que o efeito da lâmina é alterar a fase da onda. Nestas circunstâncias, pode-se afirmar que a espessura da lâmina, que provoca o deslocamento da franja central brilhante (ordem zero) para a posição que era ocupada pela franja brilhante de primeira ordem, é igual a
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Vamos começar por entender o motivo do deslocamento das franjas.
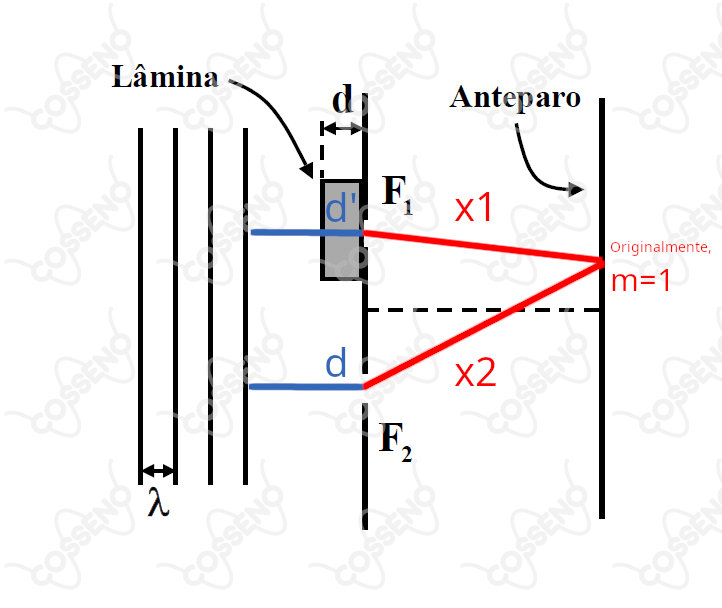 O feixe $1$ percorre a lâmina de vidro com uma velocidade menor que o feixe $2$ percorre a mesma distância (dado que o índice de refração do vidro é maior que o índice de refração do ar).
Assim, ao chegar no anteparo, o feixe $1$ terá fase diferente do feixe $2$.
Caso não existisse o vidro, teríamos um problema de fenda dupla normal:$$x_2 - x_1 = m\lambda$$
O enunciado afirma que o ponto indicado na figura corresponde ao máximo $m=1$, então:$$x_2 - x_1 = \lambda$$
Com a introdução do vidro, precisamos analisar o que ocorre antes da fenda. Precisamos considerar a diferença do caminho óptico percorrido por eles a partir do vidro.
Para que a exista interferência no ponto indicado, essa diferença de caminho deve ser igual a um múltiplo de $\lambda$, ou seja, igual a $n\lambda$, com $n$ inteiro positivo.
Assim:$$(x_2 + d) - (x_1 + d') = n\lambda$$
Como o máximo atual é $n=0$ e como $x_2 - x_1 = \lambda$, ficamos com:$$d - d' + \lambda = 0$$
De modo que $$d' - d = \lambda$$
Como o índice de refração do vidro é $1.6$, então $d' = 1{,}6d$ fazendo com que:$$d = \lambda/0{,}6 \simeq 1{,}7\lambda\Rightarrow\boxed{\text{Gab. E}}$$
O feixe $1$ percorre a lâmina de vidro com uma velocidade menor que o feixe $2$ percorre a mesma distância (dado que o índice de refração do vidro é maior que o índice de refração do ar).
Assim, ao chegar no anteparo, o feixe $1$ terá fase diferente do feixe $2$.
Caso não existisse o vidro, teríamos um problema de fenda dupla normal:$$x_2 - x_1 = m\lambda$$
O enunciado afirma que o ponto indicado na figura corresponde ao máximo $m=1$, então:$$x_2 - x_1 = \lambda$$
Com a introdução do vidro, precisamos analisar o que ocorre antes da fenda. Precisamos considerar a diferença do caminho óptico percorrido por eles a partir do vidro.
Para que a exista interferência no ponto indicado, essa diferença de caminho deve ser igual a um múltiplo de $\lambda$, ou seja, igual a $n\lambda$, com $n$ inteiro positivo.
Assim:$$(x_2 + d) - (x_1 + d') = n\lambda$$
Como o máximo atual é $n=0$ e como $x_2 - x_1 = \lambda$, ficamos com:$$d - d' + \lambda = 0$$
De modo que $$d' - d = \lambda$$
Como o índice de refração do vidro é $1.6$, então $d' = 1{,}6d$ fazendo com que:$$d = \lambda/0{,}6 \simeq 1{,}7\lambda\Rightarrow\boxed{\text{Gab. E}}$$

Ampliar Imagem


