Esboçando a situação do enunciado: 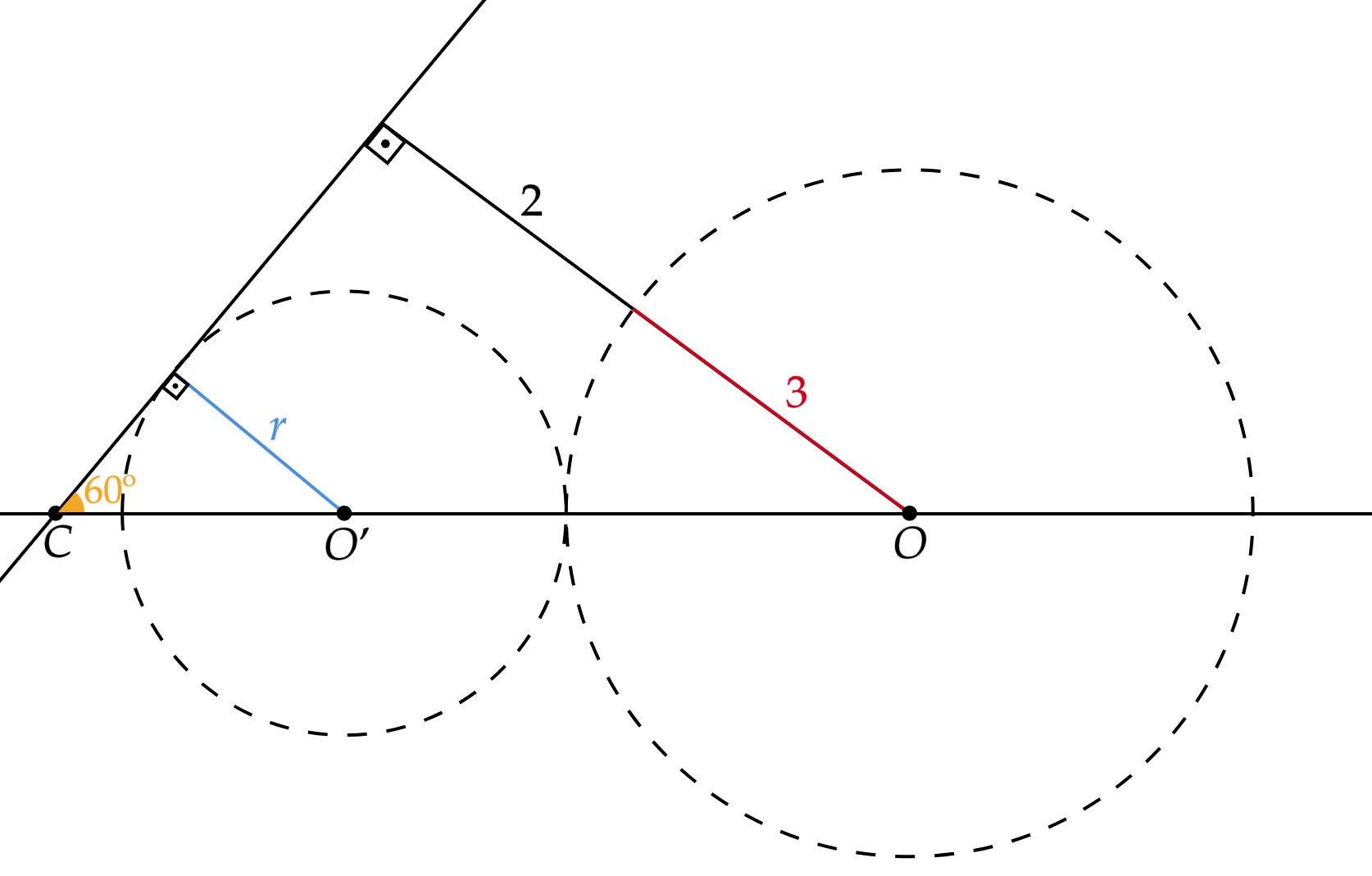Por semelhança de triângulos, têm-se:\begin{matrix} \dfrac{\overline{CO'}}{r} =\dfrac{\overline{CO}}{5} &,& \overline{CO} = \overline{CO'} + r + 3 \end{matrix}Encontrar $\overline{CO'}$ não é difícil, visto que:\begin{matrix} \sin{60^{\circ}} = \dfrac{r}{\overline{CO'}} &\therefore& \overline{CO'} = \dfrac{2r}{\sqrt{3}} \end{matrix}Substituindo os resultados acima na semelhança de triângulos:\begin{matrix} \dfrac{2}{\sqrt{3}} = \dfrac{ {2r} + r\sqrt{3} + 3\sqrt{3}}{5\sqrt{3}} &\Rightarrow& r =\dfrac{10-3\sqrt{3}}{2+\sqrt{3}} &\therefore& r = 29 - 16\sqrt{3} \ \pu{cm} \ \ \tiny{\blacksquare} \end{matrix}