A princípio, podemos esboçar a situação: 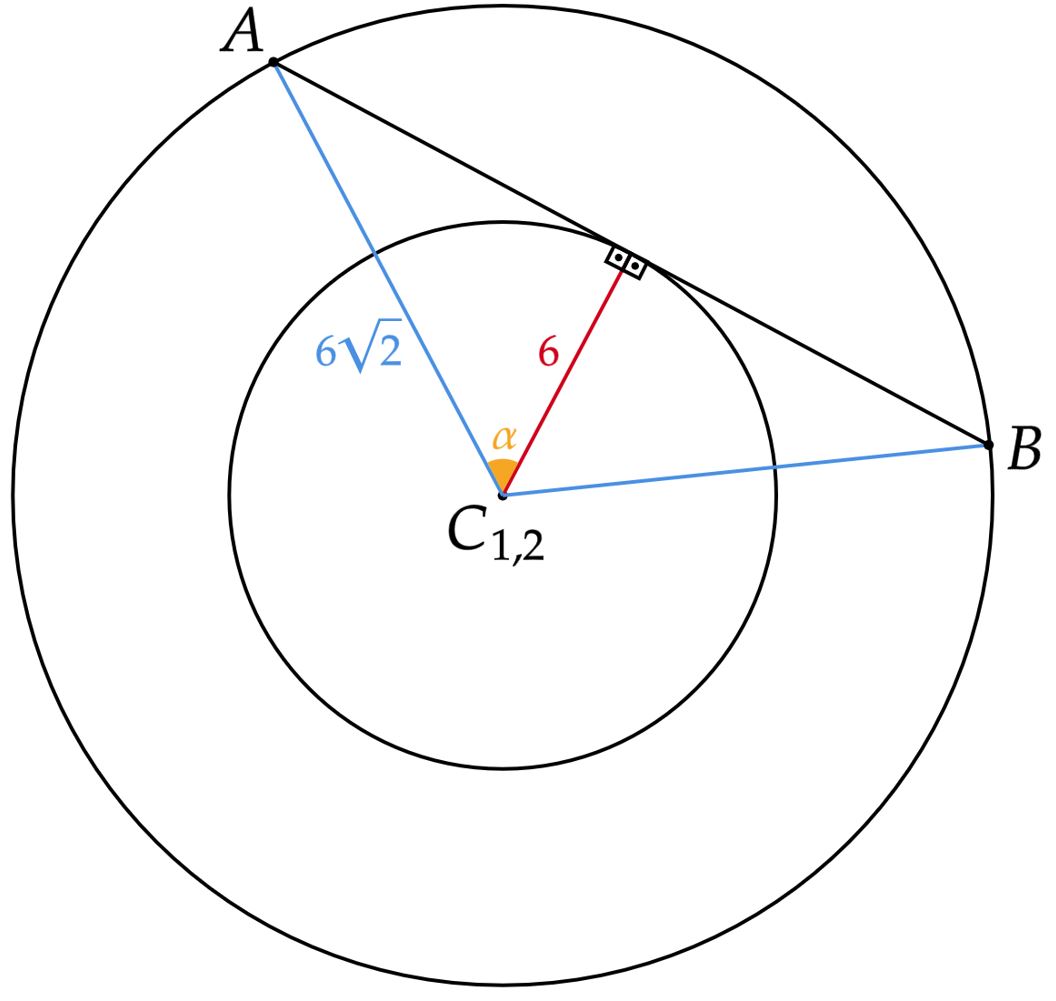Observe que a área da menor região limitada pela corda e o arco corresponde a um setor circular. Nesse sentido, vamos começar analisando o ângulo $\alpha$ da imagem, verificando o cosseno do ângulo, têm-se:\begin{matrix} \cos{\alpha} = \dfrac{6}{6\sqrt{2}} = \dfrac{\sqrt{2}}{2} &\therefore& \alpha = 45º \end{matrix}Com isso, descobrimos que os pequenos triângulos são isósceles, assim como ângulo central do setor é $90º$, ou seja, um quarto de circunferência. Dessa forma, podemos encontrar a área do setor $S$ como um quarto de circunferência menos o triângulo em questão, veja:\begin{matrix}S = \dfrac{\pi (6\sqrt{2})^2}{4} + 2 \cdot \left[\dfrac{(6\sqrt{2})(6)\sin{\alpha}}{2}\right] \\ \\ S = 18(\pi - 2) \\ \\ Letra \ (C) \end{matrix}