Pela situação descrita no enunciado, têm-se a figura abaixo: 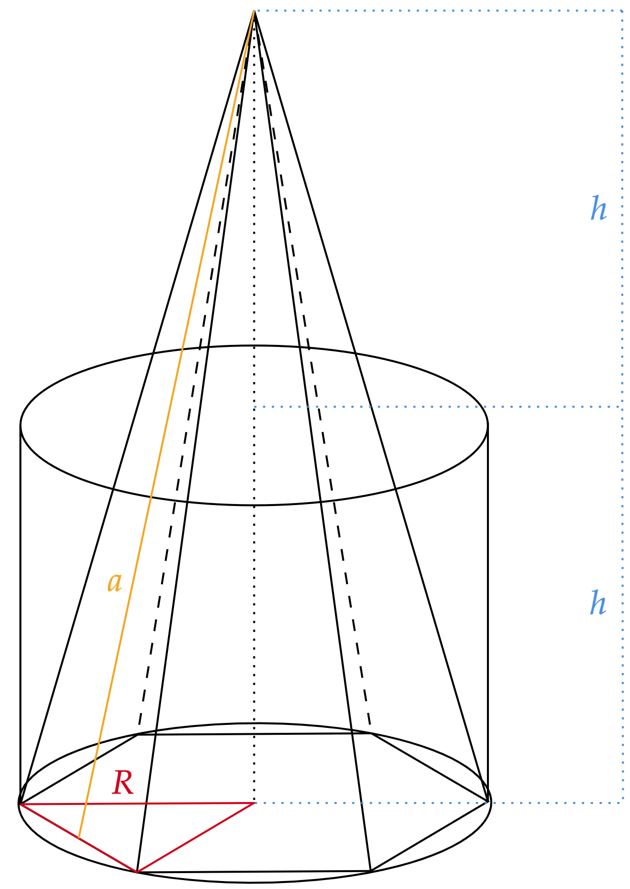Pela área total da base, encontra-se: \begin{matrix} A_{Base} = 6 \cdot {{(\dfrac{R^2\sqrt{3}}{4})}}^2 = 54\sqrt{3} &\therefore& R = 6 \ \pu{cm} \end{matrix}Continuando, pelo volume do cilindro, constata-se: \begin{matrix}V_{Cilindro} = \pi R^2 \cdot h = 360\pi &\therefore& h = 10 \ \pu{cm} \end{matrix}Pensando agora na área lateral, denotemos as arestas das faces da pirâmide de $L$, assim: \begin{matrix} L^2 = R^2 + (2h)^2 &\therefore& L = 2\sqrt{109} \ \pu{cm} \end{matrix}Com conhecimento da aresta, pode-se encontrar o apótema da pirâmide, este que será útil ao calcular a área das faces, veja: \begin{matrix} L^2 = a^2 + {{ \left(\dfrac{R}{2}\right)}}^2 &\therefore& a = \sqrt{427} \ \pu{cm} \end{matrix}Como a pirâmide apresenta seis faces triangulares, sua área lateral será:\begin{matrix} A_{Lateral} = 6 \cdot {{ \left(\dfrac{a\cdot R}{2}\right)}}^2 &\therefore& A_{Lateral} = 18\sqrt{427} \ \pu{cm^2} & \tiny{\blacksquare} \end{matrix}\begin{matrix} Letra \ (A) \end{matrix}