$• \ \text{(a):}$ Não é difícil perceber que $\overline{AC} = \overline{BC}$, ambos iguais ao raio $r$. Com isso, denotemos o centro $C: (x,y)$, novamente, não é complicado inferir que $|x| =r$, pois a circunferência é tangente ao eixo das ordenadas. Esboçando a situação descrita, 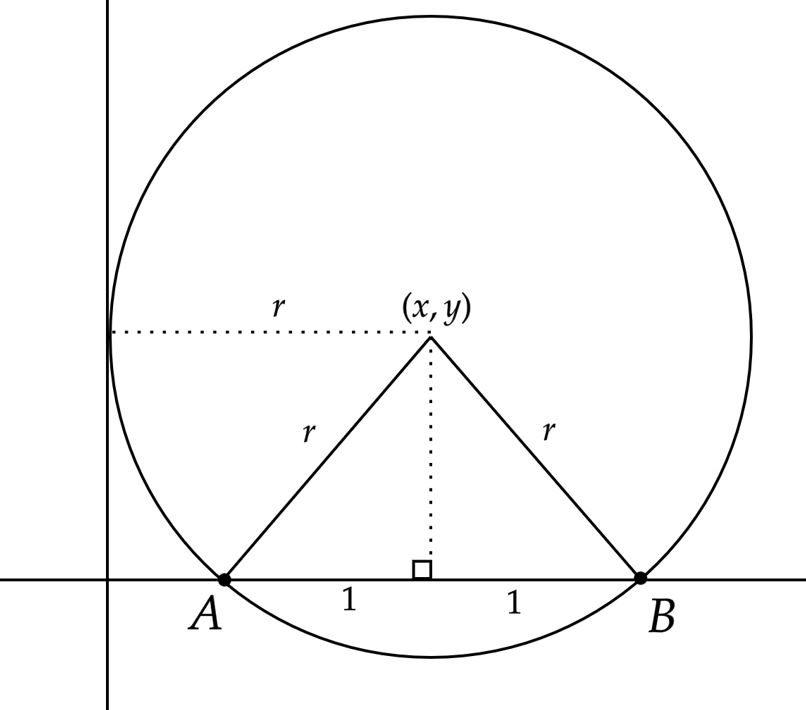Dessa forma, aplicando a $\text{Distância Euclidiana}$ pela igualdade acima, temos:\begin{matrix} (x -x_A)^2 + (y -y_A)^2 = (x -x_B)^2 + (y -y_B)^2 &\Rightarrow& (x -2)^2 + y^2 = (x -4)^2 +y^2 &\therefore& \fbox{$x=3$} \end{matrix}Baseando-se na figura, ao aplicar Pitágoras, encontramos: $\fbox{$y=2\sqrt{2}$}$ , assim, a equação da circunferência é: \begin{matrix} \pi: (x-3)^2 + (y-2\sqrt{2})^2 = 3^2 \end{matrix} $• \ \text{(b):}$ A partir do ponto $P$ é possível encontrar o coeficiente angular $(m)$, consequentemente, uma equação geral para as duas retas:\begin{matrix} m = { \dfrac{[y - (5+2\sqrt{2})]}{(x-3)}} &\Rightarrow& mx - y + (5+2\sqrt{2} - 3m) = 0 \end{matrix}Atente que, a distância entre as retas ao centro da circunferência é igual ao raio, sendo assim, \begin{matrix} r ={ \dfrac{|m(3)+(-1)(\sqrt{2}) + (5+2\sqrt{2} - 3m) |}{\sqrt{m^2 + (-1)^2}}} &\Rightarrow& 3\sqrt{m^2 + 1} = |5| &\therefore& m = \pm \dfrac{4}{3} \end{matrix}Por fim, as equações das retas são: \begin{matrix} \fbox{$\begin{matrix} 4x-3y+3+6\sqrt{2} = 0 &,& 4x-3y-27-6\sqrt{2} =0 \end{matrix}$} \end{matrix}