A questão em si é muito direta, comecemos esboçando a situação: 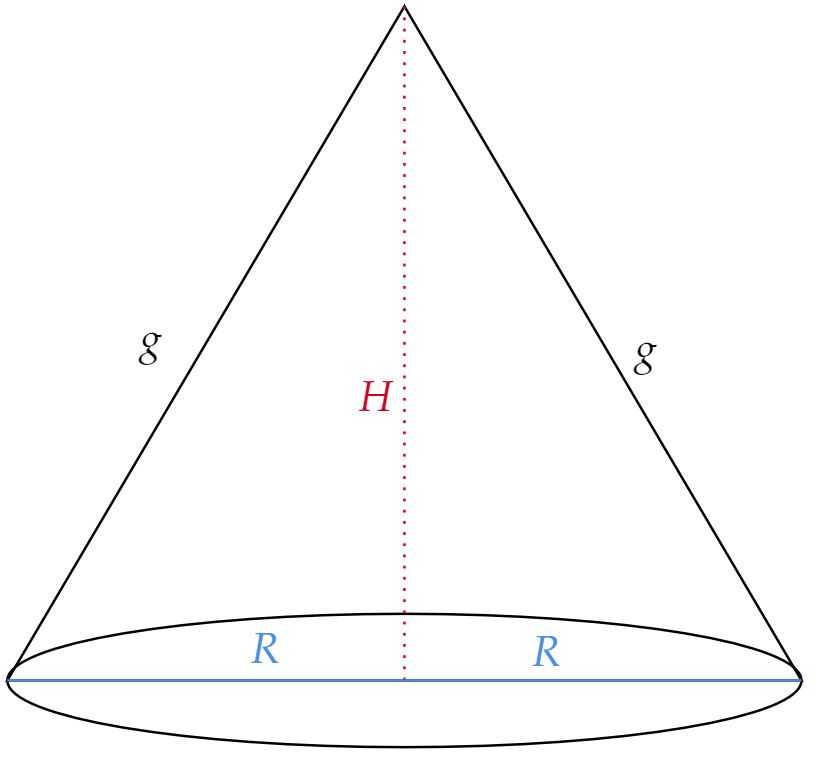Segundo enunciado, sabe-se que o semi-perímetro é igual ao raio $r$ do círculo mencionado, então: \begin{matrix} r = g+H &\Rightarrow& A_{Círculo} = \pi r^2 &\therefore& A_{Círculo} = \pi (g+H)^2 \end{matrix}Da relação fornecida pelo enunciado: \begin{matrix} {{\dfrac{A_{Círculo}}{3}}} = A_{\text{S.Cone}} &\Rightarrow& \pi (g+H)^2 = 3(\pi R^2 + \pi R g) &\therefore& \fbox{$g = 2R$} \end{matrix}Relacionando a altura, geratriz e raio do cone por Pitágoras, têm-se: \begin{matrix} g^2 = H^2 + R^2 &\Rightarrow& H^2 = 3R^2 &\therefore& \fbox{$H = R\sqrt{3}$} \end{matrix}Com isso, o volume do cone será: \begin{matrix} V = {{\dfrac{H}{3}}} \cdot (\pi R^2) &\therefore& V ={{\dfrac{1}{\sqrt{3}}}} \pi R^3 & \tiny{\blacksquare} \end{matrix}\begin{matrix} Letra \ (E) \end{matrix}