A figura mostra um sistema óptico constituído de uma lente divergente, com distância focal $f_1= − 20\ cm$ , distante $14\ cm$ de uma lente convergente com distância focal $f_2= 20\ cm$.
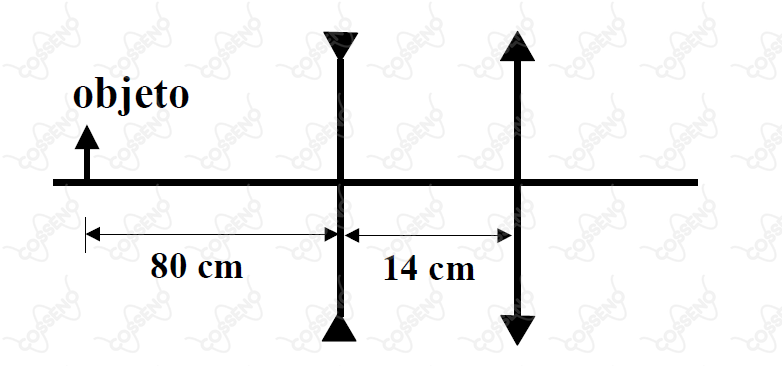
Se um objeto linear é posicionado a $80\ cm$ à esquerda da lente divergente, pode-se afirmar que a imagem definitiva formada pelo sistema
Adotando o vértice da lente divergente como o centro de um plano coordenado, temos o eixo das abcissas positivo à esquerda do vértice. Dessa forma, com conhecimento da $\text{Equação de Gauss}$, apliquemos à lente divergente para descobrir onde irá cair sua imagem conjugada:
\begin{matrix} \Large{-\frac{1}{20} = \frac{1}{80} + \frac{1}{x_i}} &\Rightarrow& \fbox{$x_i = -16 \ cm$}
\end{matrix}Perceba que a imagem $x_i$ servirá de objeto para a lente convergente, porém, repare que $x_i$ está à $(16 + 14) \ cm$ do vértice da lente convergente, a qual também aplicaremos a $\text{Equação de Gauss}$:
\begin{matrix} \Large{\frac{1}{20} = \frac{1}{30} + \frac{1}{y_i}} &\Rightarrow& \fbox{$y_i = 60 \ cm$}
\end{matrix}Agora, o "aumento linear" provocado pela lente convergente será:
\begin{matrix} A = - \Large{\frac{y_i}{(16+14)}} &\Rightarrow& \fbox{$A = -2$}
\end{matrix}Portanto, temos que o sinal negativo da expressão acima significa a imagem ser $\text{invertida}$ e, por $|A|>1$, sabemos que ela também será $\text{maior}$, além de ser $real$, vide $y_i >0$.
\begin{matrix} Letra \ (A)
\end{matrix}
