Um balão contendo gás hélio é fixado, por meio de um fio leve, ao piso de um vagão completamente fechado. O fio permanece na vertical enquanto o vagão se movimenta com velocidade constante, como mostra a figura.
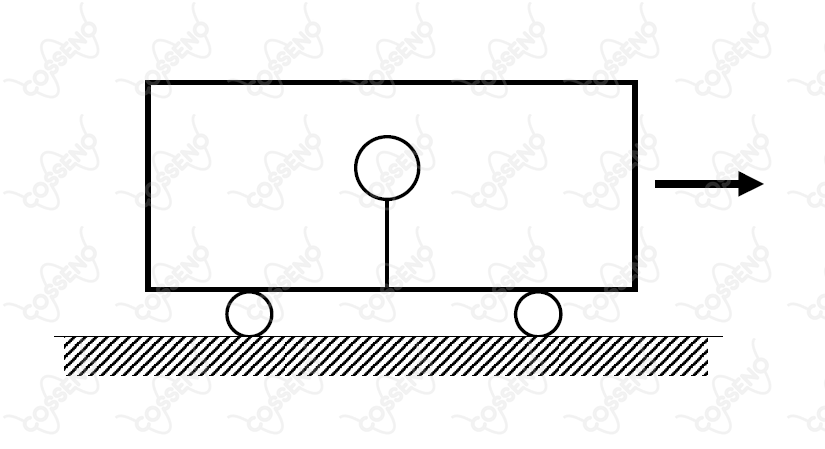
Se o vagão é acelerado para frente, pode-se afirmar que, em relação a ele, o balão
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Utilizando a teoria da relatividade de Galileu, percebe-se que a aceleração do vagão em relação à terra é computada no sentido contrário. Fazendo a soma vetorial do vetor $g$ e $-a$, obtemos um vetor aceleração resultante, como mostra a figura a seguir:
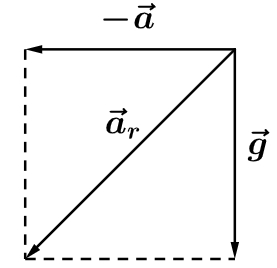 Note que como existe uma diferença de pressão, devemos considerar um novo empuxo causado pela aceleração do vagão e o movimento do balão para frente, se deve a este novo empuxo.
$\text{Situação 1}:$ Vagão se movendo com $\vec{v}$ constante, ou seja, $\vec{a} = \vec{0}$.
$$T + P = E \Rightarrow T = \rho_{ar} g V - \rho g V = (\rho_{ar} - \rho)g V.$$
Lembrando que, $\rho = \frac{m}{V} \Rightarrow m = \rho V$, então $P = mg = \rho g V.$
$\text{Situação 2}:$ Vagão se movendo com $\vec{a}$.
$$T' + P' = E' \Rightarrow T' = (\rho_{ar} - \rho)a_{r}V.$$
Como $a_{r} > g$, então $T' > T$.
$$\boxed{\text{Letra C}}$$
Note que como existe uma diferença de pressão, devemos considerar um novo empuxo causado pela aceleração do vagão e o movimento do balão para frente, se deve a este novo empuxo.
$\text{Situação 1}:$ Vagão se movendo com $\vec{v}$ constante, ou seja, $\vec{a} = \vec{0}$.
$$T + P = E \Rightarrow T = \rho_{ar} g V - \rho g V = (\rho_{ar} - \rho)g V.$$
Lembrando que, $\rho = \frac{m}{V} \Rightarrow m = \rho V$, então $P = mg = \rho g V.$
$\text{Situação 2}:$ Vagão se movendo com $\vec{a}$.
$$T' + P' = E' \Rightarrow T' = (\rho_{ar} - \rho)a_{r}V.$$
Como $a_{r} > g$, então $T' > T$.
$$\boxed{\text{Letra C}}$$

Ampliar Imagem

