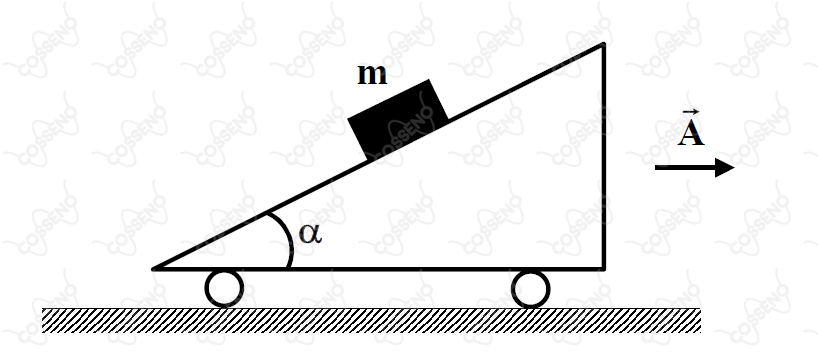
Na figura, o carrinho com rampa movimenta-se com uma aceleração constante . Sobre a rampa repousa um bloco de massa . Se é o coeficiente de atrito estático entre o bloco e a rampa, determine o intervalo para o módulo de , no qual o bloco permanecerá em repouso sobre a rampa.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Utilizando o princípio da equivalência, podemos esboçar as forças que atuam no bloco como:
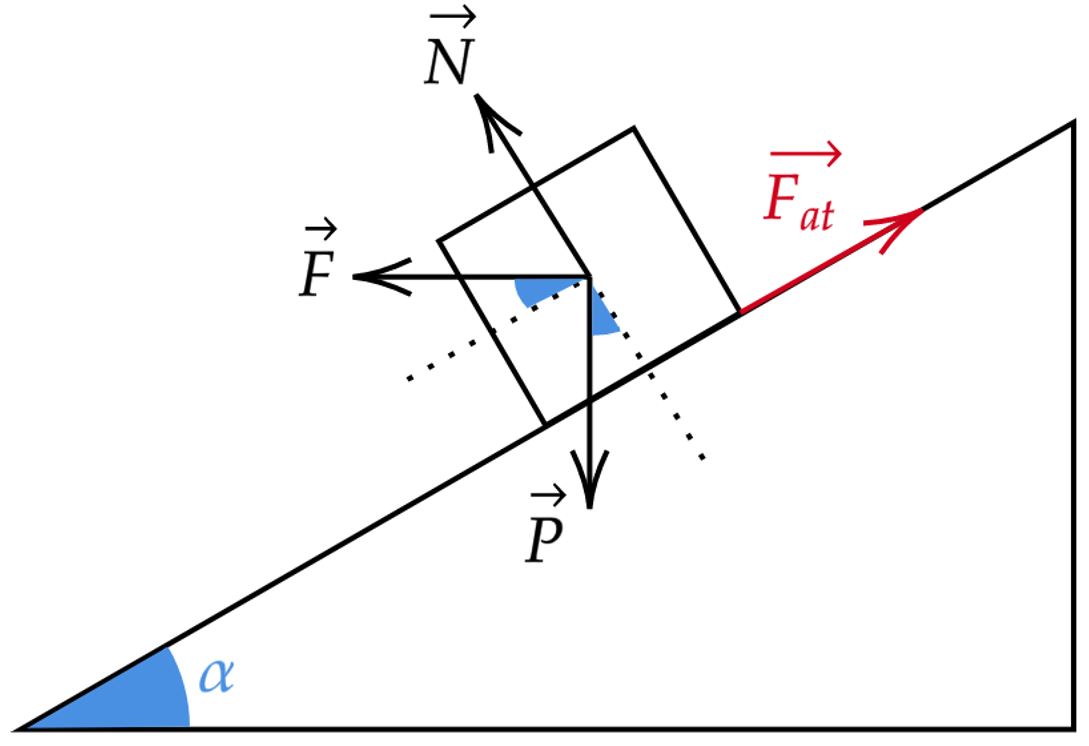 Observe que $\vec{F}$ é a nossa força fictícia devido a aceleração do carrinho. Nesse contexto, vamos decompor as forças e escrever:\begin{matrix}
\begin{cases} N + F\sin{\alpha} &=& P\cos{\alpha} \\
P\sin{\alpha}+ F\cos{\alpha} &=& F_{at}
\end{cases} \end{matrix}Com conhecimento que $F_{at} \le \mu N$, temos:\begin{matrix}
P\sin{\alpha}+ F\cos{\alpha} \le \mu(P\cos{\alpha} - F\sin{\alpha}) \\
\end{matrix}Como $P = mg$ e $F=mA$, têm-se:\begin{matrix}
g\sin{\alpha}+ A\cos{\alpha} \le \mu(g\cos{\alpha} - A\sin{\alpha}) \\ \\
A(\cos{\alpha} + \mu \sin{\alpha}) \le g(\mu \cos{\alpha} - \sin{\alpha}) \\ \\
0 \le A \le g \left(\dfrac{\mu \cos{\alpha} - \sin{\alpha}}{\cos{\alpha} + \mu \sin{\alpha}} \right)
\end{matrix}Analisando as condições da expressão acima, conseguimos determinar o intervalo para o módulo de $\vec{A}$ como:\begin{matrix}
|\vec{A}| \in \left[ 0 \ , \ g \left(\dfrac{\mu \cos{\alpha} - \sin{\alpha}}{\cos{\alpha} + \mu \sin{\alpha}} \right) \right] &,& \mu \cos{\alpha} > \sin{\alpha}
\end{matrix}
Observe que $\vec{F}$ é a nossa força fictícia devido a aceleração do carrinho. Nesse contexto, vamos decompor as forças e escrever:\begin{matrix}
\begin{cases} N + F\sin{\alpha} &=& P\cos{\alpha} \\
P\sin{\alpha}+ F\cos{\alpha} &=& F_{at}
\end{cases} \end{matrix}Com conhecimento que $F_{at} \le \mu N$, temos:\begin{matrix}
P\sin{\alpha}+ F\cos{\alpha} \le \mu(P\cos{\alpha} - F\sin{\alpha}) \\
\end{matrix}Como $P = mg$ e $F=mA$, têm-se:\begin{matrix}
g\sin{\alpha}+ A\cos{\alpha} \le \mu(g\cos{\alpha} - A\sin{\alpha}) \\ \\
A(\cos{\alpha} + \mu \sin{\alpha}) \le g(\mu \cos{\alpha} - \sin{\alpha}) \\ \\
0 \le A \le g \left(\dfrac{\mu \cos{\alpha} - \sin{\alpha}}{\cos{\alpha} + \mu \sin{\alpha}} \right)
\end{matrix}Analisando as condições da expressão acima, conseguimos determinar o intervalo para o módulo de $\vec{A}$ como:\begin{matrix}
|\vec{A}| \in \left[ 0 \ , \ g \left(\dfrac{\mu \cos{\alpha} - \sin{\alpha}}{\cos{\alpha} + \mu \sin{\alpha}} \right) \right] &,& \mu \cos{\alpha} > \sin{\alpha}
\end{matrix}

Ampliar Imagem

