No Laboratório de Plasmas Frios do ITA é possível obter filmes metálicos finos, vaporizando o metal e depositando-o por condensação sobre uma placa de vidro. Com o auxílio do dispositivo mostrado na figura, é possível medir a espessura de cada filme. Na figura, os dois geradores são idênticos, de f.e.m. e resistência , estando ligados a dois eletrodos retangulares e paralelos, e , de largura e separados por uma distância .
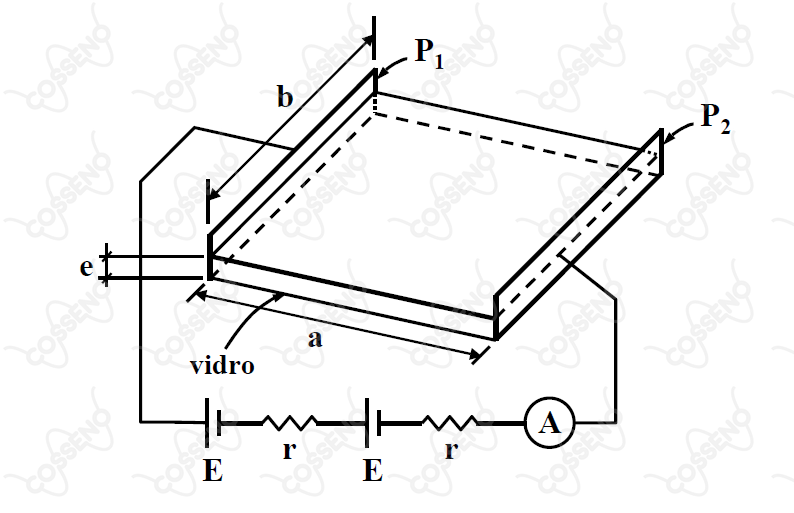
Um amperímetro ideal é inserido no circuito, como indicado. Supondo que após certo tempo de deposição é formada sobre o vidro uma camada uniforme de alumínio entre os eletrodos, e que o amperímetro acusa uma corrente , qual deve ser a espessura do filme?
Resistividade do alumínio: $\rho = 2{,}6 \times {10}^{-8}\ \Omega\cdot m$
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Assumindo que o alumínio preencha todo volume da placa, formando um condutor de resistência $R$, pode-se começar pela $\text{Lei de Pouillet}$: \begin{matrix} i = {\dfrac{2E}{(2r + R)}} &\Rightarrow& 0,10 = {\dfrac{2\cdot 2}{(2\cdot 1 + R)}} &\therefore& R = 38 \ \Omega
\end{matrix}A partir da resistência, com conhecimento da $\text{Segunda lei de Ohm}$, têm-se: \begin{matrix}
R = {{\dfrac{\rho \cdot a}{b\cdot e}}} = {{\dfrac{(2,6\cdot 10^{-8}) \cdot (3\cdot 10^{-2})}{(1\cdot10^{-2})\cdot e}}} = 38 &\therefore& \fbox{$ e = 4,\bar{3} \cdot 10^{-9} \ \pu{m} $}
\end{matrix}\begin{matrix} Letra \ (C)
\end{matrix}

