A partir do repouso, uma pedra é deixada cair da borda no alto de um edifício. A figura mostra a disposição das janelas, com as pertinentes alturas e distâncias que se repetem igualmente para as demais janelas, até o térreo.
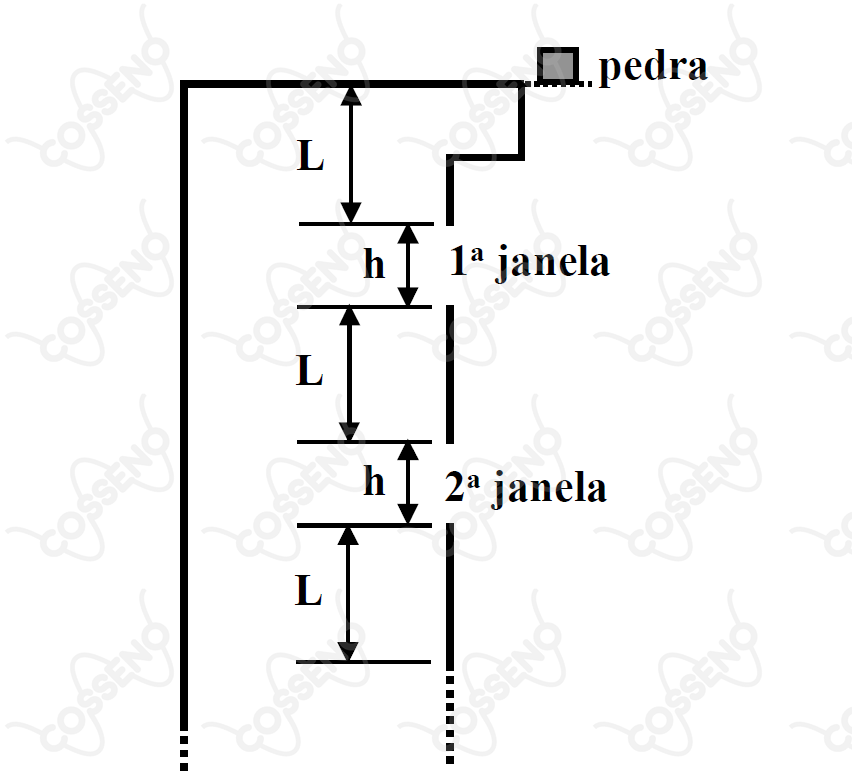
Se a pedra percorre a altura h da primeira janela em segundos, quanto tempo levará para percorrer, em segundos, a mesma altura da quarta janela? (Despreze a resistência do ar).
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Utilizando como base a relação $S = \dfrac{gt^2}{2}$ , podemos escrever que o tempo $t$ necessário para percorrer a janela $1$ é dada por
$t = \sqrt{\dfrac{2(L + h)}{g}} - \sqrt{\dfrac{2L}{g}} =t= \dfrac{\sqrt{2}}{\sqrt{g}}\left(\sqrt{L + h} - \sqrt{L}\right)$
Utilizando o mesmo raciocínio para a ánalise da janela $4$ temos que o tempo $T$ para percorre-lo será dado por
$T= \dfrac{\sqrt{2}}{\sqrt{g}}\left(\sqrt{4L + 4h} - \sqrt{4L + 3h}\right)$
$\therefore$
$T=\dfrac{t}{\left(\sqrt{L + h} - \sqrt{L}\right)} \cdot \left(\sqrt{4L + 4h} - \sqrt{4L + 3h}\right)$
$ = T = t \left(\dfrac{\sqrt{4L + 4h} - \sqrt{4L + 3h}}{\sqrt{L + h} - \sqrt{L}}\right) $
$= \boxed{T =t \left(\dfrac{\sqrt{4(L + h)} - \sqrt{3(L+h) + L}}{\sqrt{L + h} - \sqrt{L}}\right) }$
$\textbf{Resposta : Alternativa C}$
Pensando na equação horária a partir do repouso, temos:\begin{matrix}
\Delta y = \dfrac{g\Delta t^2}{2}&,& \dfrac{g}{2} = k &\Rightarrow& \Delta y = k \Delta t^2
\end{matrix}Agora, vamos começar encontrando $t$, este deve ser a diferença de dois momentos $t_1$ e $t_2$:\begin{matrix}\begin{cases}
\ \ \ \ L &=&k \cdot (t_1)^2 \\
L+h &=& k \cdot (t_2)^2
\end{cases} &,& t_2 - t_1 = t &\therefore& t = \sqrt{\dfrac{1}{k}} \cdot (\sqrt{L+h} - \sqrt{L})
\end{matrix}Com isso, vamos assumir um raciocínio semelhante para a quarta janela, em que:\begin{matrix}\begin{cases}
4L+3h &=&k \cdot (t_3)^2 \\
4L+4h &=& k \cdot (t_4)^2
\end{cases} &,& t_4 - t_3 = t_h
\end{matrix}Analogamente,\begin{matrix} t_h = \sqrt{\dfrac{1}{k}} \cdot (\sqrt{4(L+h)} - \sqrt{4L + 3h})
\end{matrix}Por fim, vamos isolar $(\sqrt{k})^{-1}$ em $t$ e substituir no nosso resultado acima:\begin{matrix} t_h = \left( \dfrac{\sqrt{4(L+h)} - \sqrt{4L + 3h}}{(\sqrt{L+h} - \sqrt{L}} \right)t
\end{matrix}\begin{matrix}Letra \ (C)
\end{matrix}


