Variações no campo gravitacional na superfície da Terra podem advir de irregularidades na distribuição de sua massa. Considere a Terra como uma esfera de raio e de densidade , uniforme, com uma cavidade esférica de raio , inteiramentente contida no seu interior. A distância entre os centros , da Terra, e , da cavidade, é , que pode variar de (zero) até , causando, assim, uma variação do campo gravitacional em um ponto , sobre a superfície da Terra, alinhado com e . (Veja a figura)
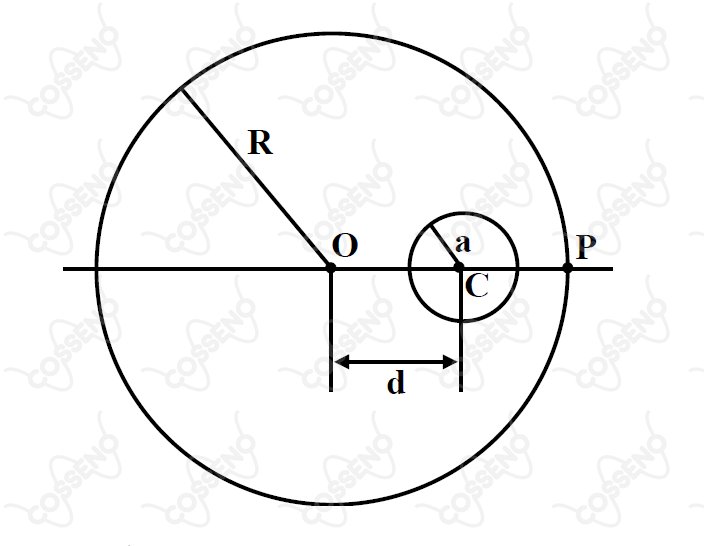
Seja a intensidade do campo gravitacional em sem a existência da cavidade na Terra, e , a intensidade do campo no mesmo ponto, considerando a existência da cavidade. Então, o valor máximo da variação relativa: , que se obtém ao deslocar a posição da cavidade, é
CossenoGPT


