A figura mostra dois capacitores, $1$ e $2$, inicialmente isolados um do outro, carregados com uma mesma carga $Q$.
A diferença de potencial (ddp) do capacitor $2$ é a metade da ddp do capacitor $1$. Em seguida, as placas negativas dos capacitores são ligadas à Terra e, as positivas, ligadas uma a outra por um fio metálico, longo e fino. Pode-se afirmar que
Seja $C_1$ a capacitância do capacitor $1$, e $C_2$ a capacitância do capacitor $2$, então: \begin{matrix} C_1 = {{\dfrac{Q}{V_1}}} &,& C_2 = {{\dfrac{2Q}{V_1}}}
\end{matrix}Ao ligar os capacitores a terra do modo informado, têm-se:
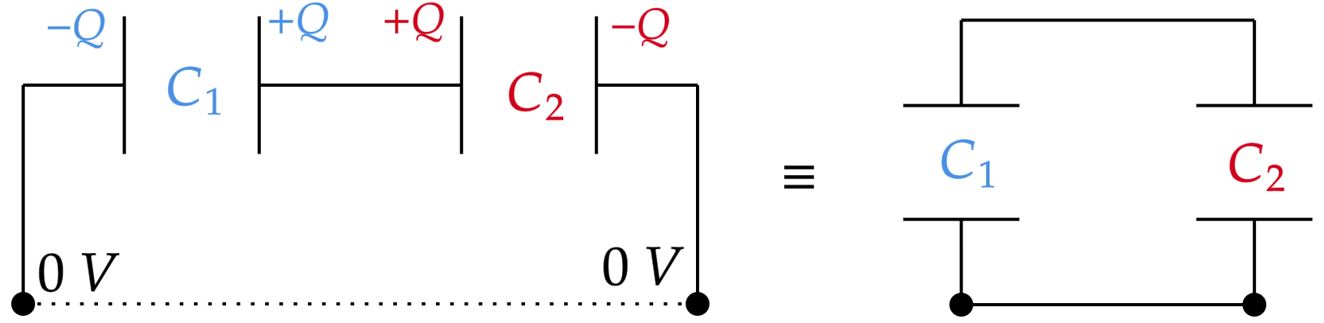Percebe-se assim uma associação de capacitores em paralelo, em que a capacitância equivalente será: \begin{matrix} C_{eq} = C_1 + C_2 &\therefore& C_{eq} = 3C_1
\end{matrix}Agora, analisando as alternativas:
$• \ \text{Alternativa (A):}$ $\color{orangered}{\text{Incorreta}}$
Não, é o inverso.
$• \ \text{Alternativa (B):}$ $\color{orangered}{\text{Incorreta}}$
Certamente elas continuam as mesmas.
$• \ \text{Alternativa (C):}$ $\color{orangered}{\text{Incorreta}}$
Observe as figuras acima, os potenciais serão iguais.
$• \ \text{Alternativa (D):}$ $\color{royalblue}{\text{Correta}}$
Pela conservação da carga elétrica: \begin{matrix} Q_{eq} = Q_1 + Q_2 &\therefore& Q_{eq} = 2Q
\end{matrix}Continuando,\begin{matrix} {{\dfrac{V_{eq}}{V_{1}}}} = {{\dfrac{\dfrac{2Q}{3C_1}}{\dfrac{Q}{C_1}} }} = {{\dfrac{2}{3}}} &\therefore& V_{eq } = {{\dfrac{2}{3}}} \cdot V_1 &\tiny{\blacksquare}
\end{matrix}
$• \ \text{Alternativa (E):}$ $\color{orangered}{\text{Incorreta}}$
Na verdade é três vezes.
\begin{matrix} Letra \ (D)
\end{matrix}
Ampliar Imagem
