$• \ \text{Resolução I:}$ $\color{royalblue}{\text{Pappus–Guldin}}$ Seguindo o comando da questão, podemos pensar num plano cartesiano, veja: 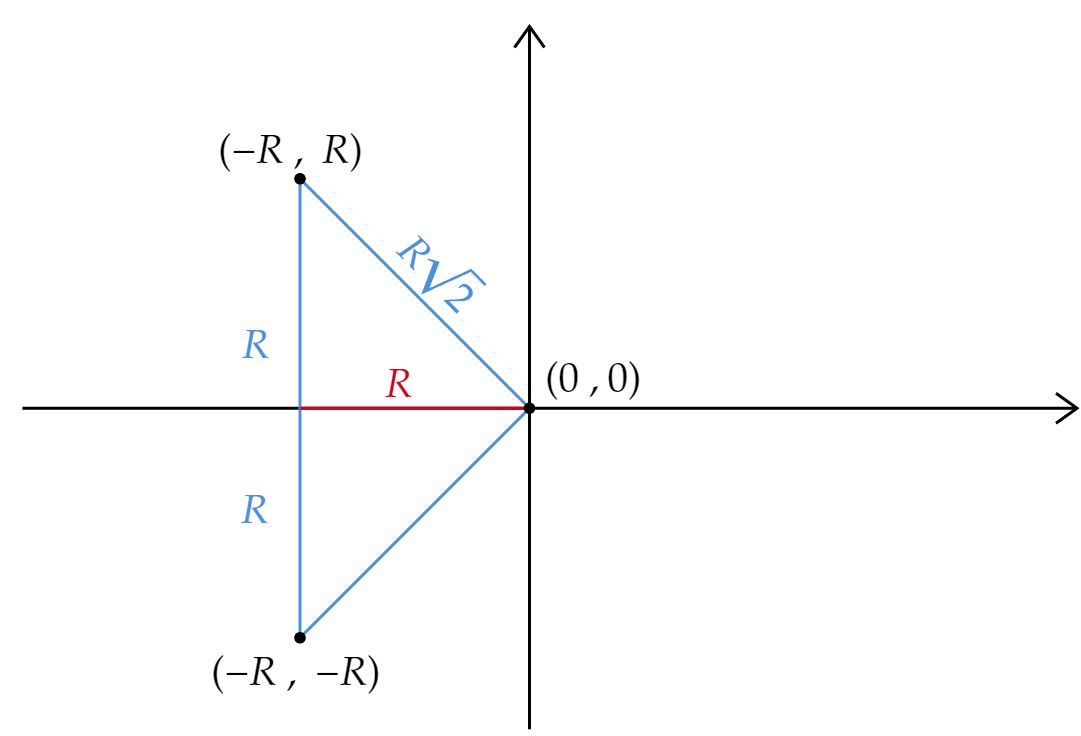Por geometria analítica ou plana, precisamos da distância do vértice $O$ ao baricentro, pois iremos utilizar do teorema de Pappus–Guldinus. Desse modo, por geometria analítica, esta distância é:\begin{matrix} x_G = {{ \left(\dfrac{0 - R - R }{3} \right)}} &\therefore& |x_G| = {{\dfrac{2R}{3}}} \end{matrix}Continuando, precisamos ainda da área do triângulo $(A)$, o que não é difícil, por isso, pelo teorema de Pappus–Guldin, têm-se: \begin{matrix} V = 2\pi \cdot|x_G| \cdot A &\Rightarrow& V = 2\pi \cdot \left({{\dfrac{2R}{3}}}\right) \cdot \left[ {{\dfrac{(2R)(R)}{2}}}\right] &\therefore& V = {{\dfrac{4\pi}{3}}}R^3 & \tiny{\blacksquare} \end{matrix} $• \ \text{Resolução II:}$ $\color{royalblue}{\text{Diferença de volumes}}$ Atente que, ao rotar o triângulo da maneira descrita, irá se formar um cilindro vazado de dois cones idênticos de altura $R$ e raio da base $R$. Nessa perspectiva, comecemos pelo volume do cilindro, ele será: \begin{matrix} V_{\text{Cilindro}} = \pi R^2 \cdot2R &\therefore& V_{\text{Cilindro}} = 2\pi R^3 \end{matrix}Agora, o volume de um dos cones:\begin{matrix} V_{\text{Cone}} = {{\dfrac{R}{3} }}\cdot \pi R^2 &\therefore& V_{\text{Cone}} = {{\dfrac{\pi R^3}{3}}} \end{matrix}Então, o volume solicitado será:\begin{matrix} V = V_{\text{Cilindro}} - 2V_{\text{Cone}} &\therefore& V = {{\dfrac{4\pi}{3}}}R^3 & \tiny{\blacksquare} \end{matrix}\begin{matrix} Letra \ (C) \end{matrix}