Sejam e duas retas paralelas distando entre si . Seja um ponto na região interior a estas retas, distando de r. A área do triangulo eqüilátero , cujos vértices e estão, respectivamente, sobre as retas e , é igual, em , a:
CossenoGPT
Teste
gratuitamente agora
mesmo! 
Esboçando a situação:
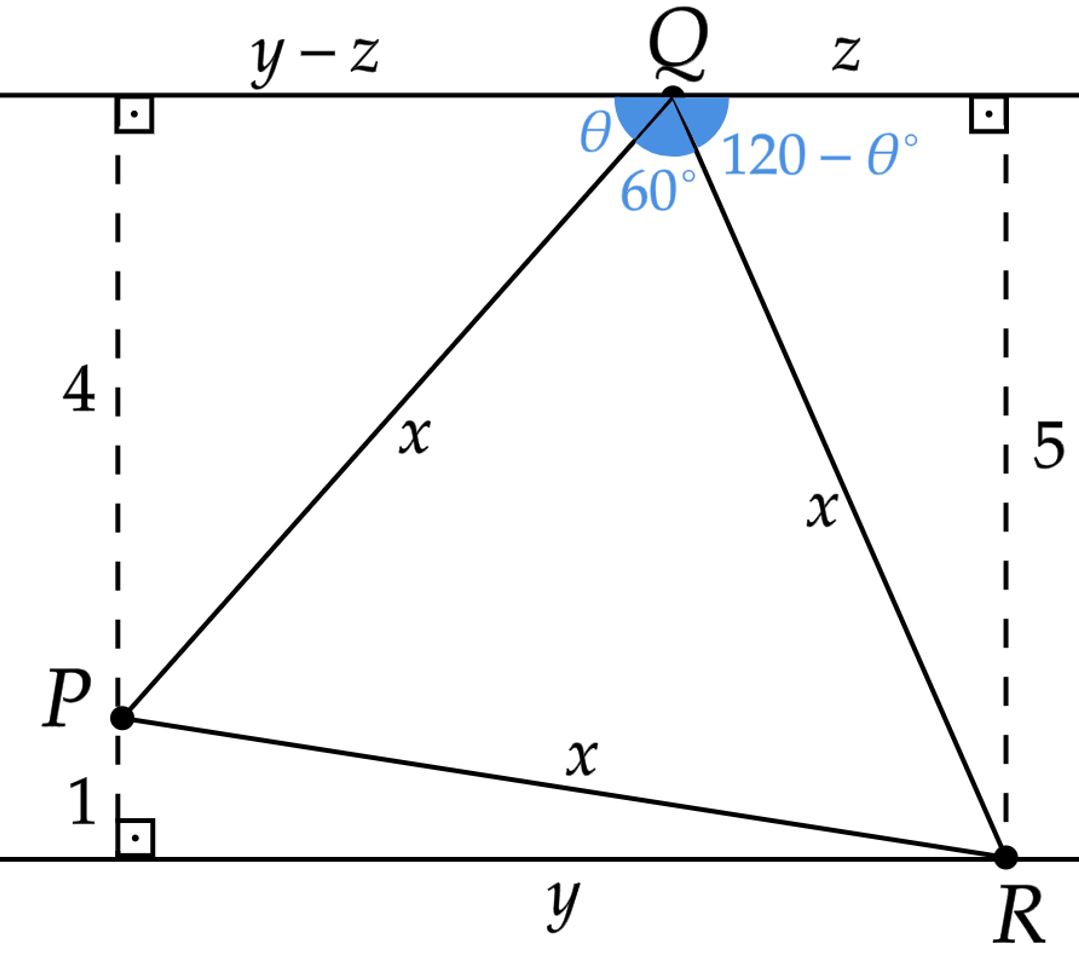Nesse contexto, podemos escrever:\begin{matrix}
\sin{(120º -\theta)} &=& \sin{(120º)}\cos{(\theta)} - \sin{(\theta)}\cos{(120º)} &=& \dfrac{5}{x}
\end{matrix}Com isso,\begin{matrix}\dfrac{\sqrt{3}}{2} \cdot \dfrac{y-z}{x} - \dfrac{4}{x} \left(-\dfrac{1}{2}\right) = \dfrac{5}{x} &\Rightarrow&
(y-z) = 2\sqrt{3}
\end{matrix}Agora, utilizando o teorema de Pitágoras:\begin{matrix} x^2 = 4^2 +(y-z)^2 &\Rightarrow& x^2 = 28
\end{matrix}Por fim, a área de do triângulo equilátero:\begin{matrix}[PQR] = \dfrac{x^2\sqrt{3}}{4} &\therefore& [PQR] = 7\sqrt{3} \ \pu{cm^2} & \tiny{\blacksquare}
\end{matrix}\begin{matrix}Letra \ (B)
\end{matrix}
Ampliar Imagem
