Considere a família de circunferências com centros no segundo quadrante e tangente ao eixo . Cada uma destas circunferências corta o eixo em dois pontos, distantes entre si de . Então, o lugar geométrico dos centros desta circunferências é parte:
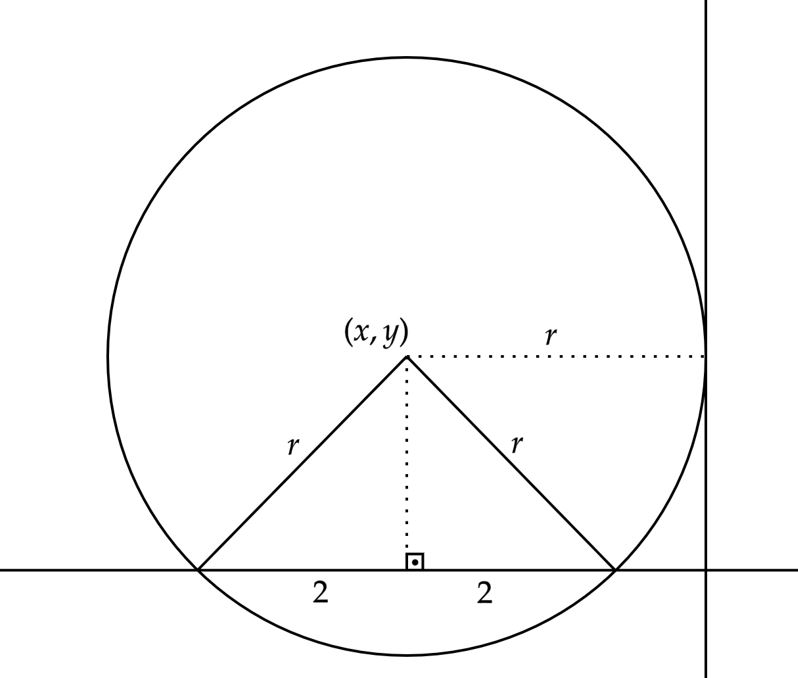
Considere o centro da circunferência em $C:(x,y)$ e raio $r$, esboçando a situação não é difícil encontrar um triângulo retângulo (ver figura), este que nos fornece a relação: \begin{matrix} r^2 = y^2 + 2^2
\end{matrix}Atente que, a circunferência é tangente ao eixo dar ordenadas, sendo obrigatoriamente $|x| =r$, substituindo na equação acima:
\begin{matrix} {\dfrac{(x-0)^2}{2^2} - \dfrac{(y-0)^2}{2^2}} & =& 1
\end{matrix}Portanto, constata-se uma $\text{hipérbole}$ com abertura leste-oeste, esta que está centrada na origem, com semi-eixos iguais a $2$
\begin{matrix} Letra \ (C)
\end{matrix}
Ampliar Imagem
