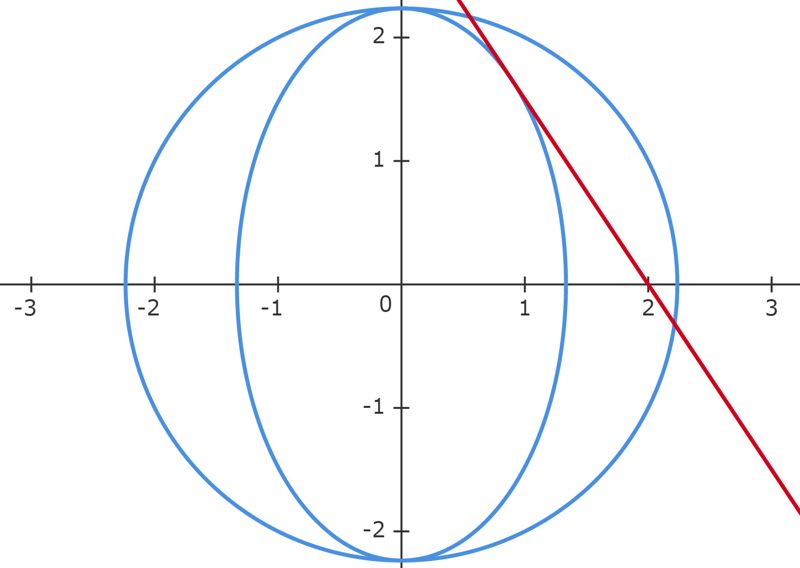
Sabe-se que uma elipse de equação tangencia internamente a circunferência de equação e que a reta de equação é tangente à elipse no ponto . Determine as coordenadas de .
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A priori, analisando a reta junto a circunferência, isto é, esboçando, não é difícil perceber que temos necessariamente $\fbox{$b^2 = 5$}$, pois o centro das duas cônicas coincidem em $(0,0)$, com a elipse possuindo eixo maior nas ordenadas, visto que do contrário, não teríamos o ponto de tangência. Nessa perspectiva, isolando $x$ ou $y$ na equação da reta, e substituindo na equação da elipse, deve-se apresentar uma equação de segundo grau, a qual possui determinante igual a zero, vide o ponto de tangência. Enfim, a rigor, isolemos $y$:
\begin{matrix} y = \dfrac{3}{2}(2-x) &\Rightarrow& \dfrac{x^2}{a^2} + \dfrac{3^2(2-x)^2}{4.5} = 1 \ \ \color{royalblue}{\text{(I)}} &\Rightarrow& x^2(20+9a^2)-36a^2x+16a^2=0
\end{matrix} Como $\Delta =0$ \begin{matrix}36^2a^4-4(16a^2)(20+9a^2)=0 &\therefore& a^2 = {\dfrac{4^2}{3^2}}
\end{matrix}Substituindo $a^2$ em $\text{(I)}$, facilmente encontramos $x_P$, e consequentemente $y_P$,
\begin{matrix} x_P = \dfrac{8}{9} &,& y_P = \dfrac{5}{3} &\therefore& \fbox{$P: \left(\dfrac{8}{9} \ , \ \dfrac{5}{3} \right)$}
\end{matrix}

Ampliar Imagem

14:02 21/02/2024
Fala amigo, bom dia. Você errou alguma conta após substituir a² na equação (I). As resposta seria P:(8/9, 5/3)

