Segundo enunciado, $w \in \mathbb{R}$, logo: \begin{matrix} \color{royalblue}{(1)}: (z + \bar{z} + 2) \in \ \mathbb{R} &&,&& \color{royalblue}{(2)}: (\sqrt{|z-1| + |z+1| - 3}) \in \ \mathbb{R} \end{matrix}Note que, rapidamente, pode-se inferir que a preposição $(1)$ é verdadeira, para isso, basta representar $z$ como $x+yi$, veja: \begin{matrix} (z + \bar{z} + 2) = (x+yi + x -yi +2) = 2x + 2 &|& x\in \mathbb{R} &\therefore& (1) \in \ \mathbb{R} \end{matrix}Com isso, percebe-se que a questão se restringe a análise do denominador $(2)$, dele, têm-se:\begin{matrix}\sqrt{|z-1| + |z+1| - 3} > 0 &\Rightarrow& |z-1| + |z+1| > 3 & \color{royalblue}{(3)} \end{matrix}Nesse momento, deve-se interpretar $(3)$ geometricamente, num tratamento lexical, o que a equação nos diz é: a soma da distância $|z-1|$ mais a distância $|z+1|$ é maior que $3$. Desse modo, com conhecimento de $\text{elipses}$, não é difícil dizer que se refere a relação fundamental de simetria da mesma, comumente escrita como: \begin{matrix} \overline{PF_1} &+& \overline{PF_2} &=& 2a \end{matrix}Pensando em números complexos, esta relação pode ser expressa como: \begin{matrix} |z - z_1| &+& |z - z_2| &=& 2a\end{matrix}Em que $z_1$ e $z_2$ são pontos fixos e representam as posições dos focos. Nesse viés, analisando $(3)$ têm-se: \begin{matrix}z_1 = 1 + 0i = (1,0) &,& z_2 = -1 + 0i = (-1,0) &,&2a = 3 \end{matrix}Novamente, noutro tratamento lexical, pode-se dizer que a expressão $(3)$ diz respeito à todos os pontos externos a elipse de eixo maior $3$, e focos em $(1,0)$ e $(-1,0)$ - certamente centrada na origem. 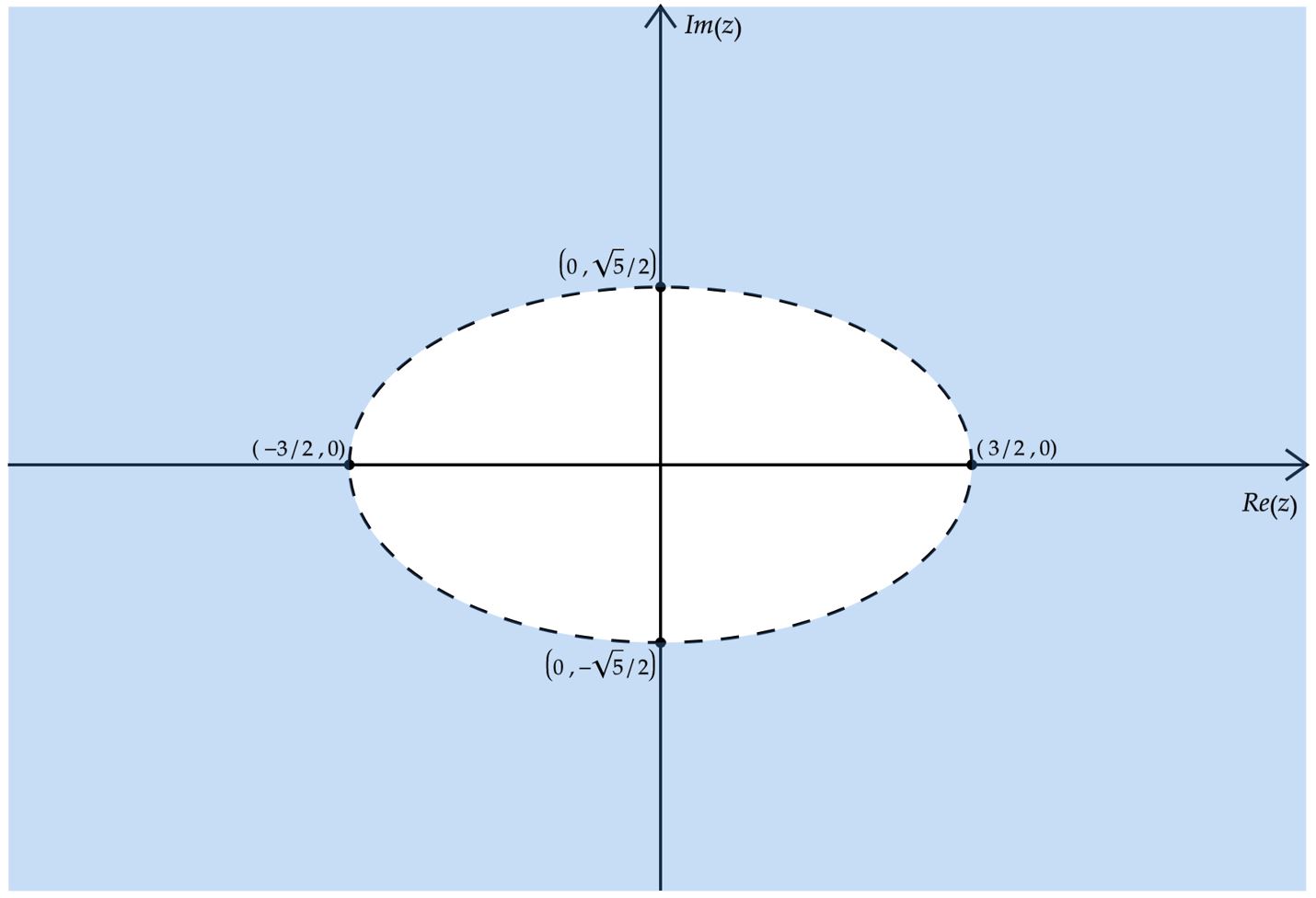Sabida a relação pitagórica da elipse, sem muitos problemas pode-se encontrar o valor do semi-eixo menor $b$, veja: \begin{matrix} c: \text{metade da distância focal} &|& a^2 = b^2 + c^2 &,& c = 1 &\therefore& b= \dfrac{\sqrt{5}}{2} \end{matrix}Por fim, numa representação gráfica, têm-se: