Considere uma pirâmide regular de altura igual a e cuja base é formada por um quadrado de área igual a . A distância de cada face desta pirâmide ao centro de sua base, em , é igual a:
CossenoGPT
Teste
gratuitamente agora
mesmo! 
Como a área da base é $8 \ cm^2$, certamente a aresta da base será $2\sqrt{2} \ cm$. Nessa perspectiva, denotemos o apótema da pirâmide de $a$, assim, têm-se a figura:
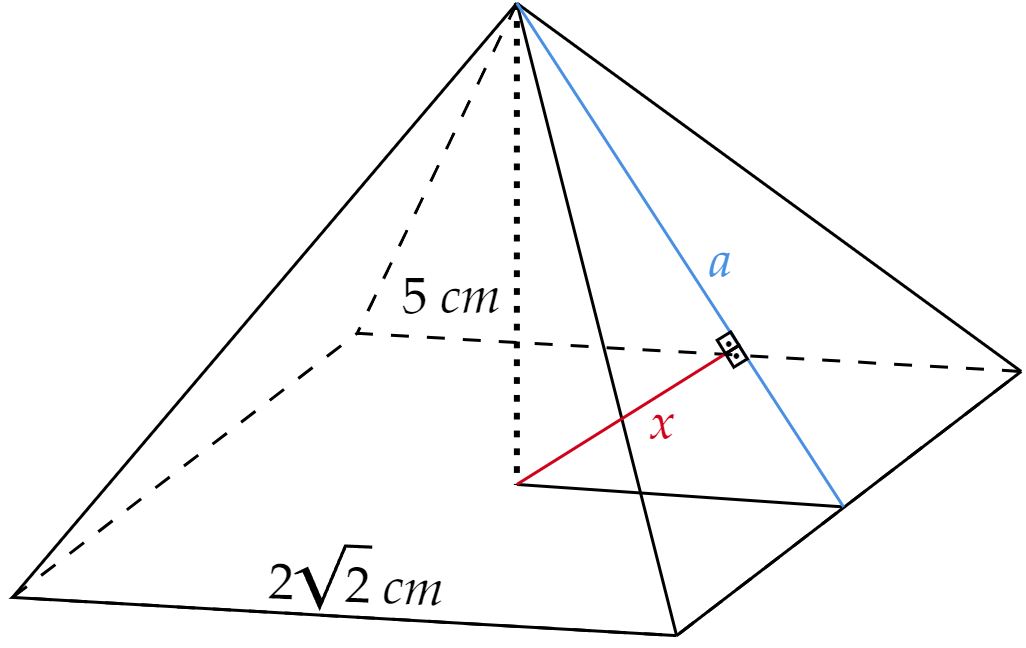Atente que, por Pitágoras, encontra-se: \begin{matrix} a^2 = (\sqrt{2})^2 + (5)^2 &\therefore& a =3\sqrt{3} \ \pu{cm}
\end{matrix}Com isso, por uma semelhança de triângulos: \begin{matrix}
{{\dfrac{x}{5}}} = {{\dfrac{\sqrt{2}}{a}}} &\therefore& x = {{\dfrac{5\sqrt{6}}{9}}} \ \pu{cm} & \tiny{\blacksquare}
\end{matrix}\begin{matrix} Letra \ (B)
\end{matrix}
Ampliar Imagem
