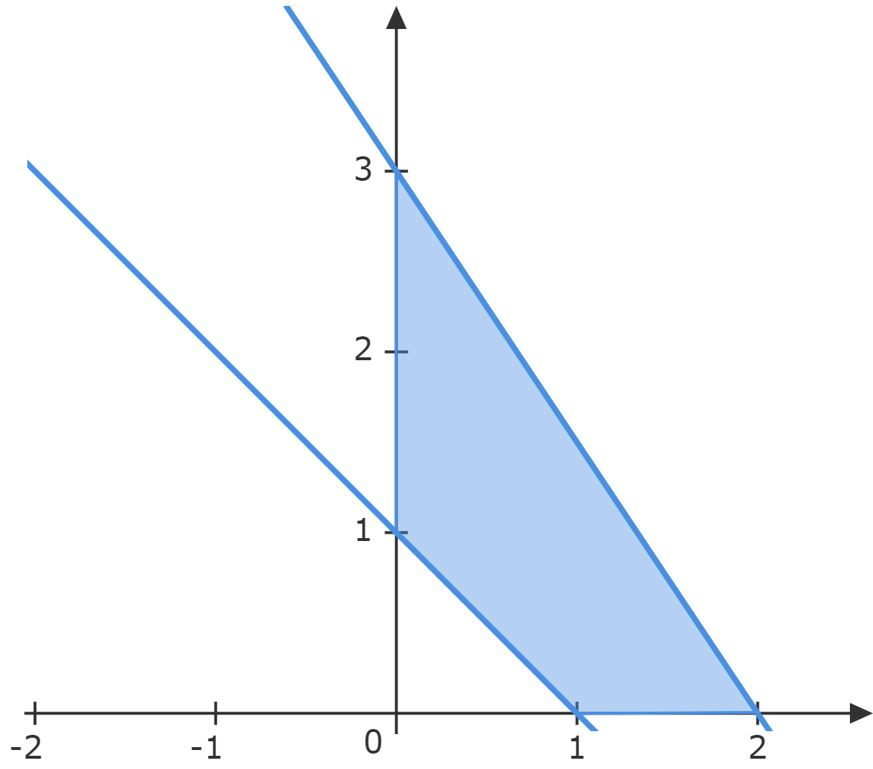
$• \ \text{Resolução I:}$ A área do polígono é determinado pelos eixos coordenados, logo, fazendo respectivamente, $x=0$ e $y=0$ no conjunto: \begin{matrix} y^2-4y+3 = 0 &&,&& x^2-3x+2 = 0 \\ \\ y_1 = 1 \ \ \vee \ \ y_2 = 3 &&&& x_1 = 1 \ \ \vee \ \ x_2 = 2 \end{matrix}Têm-se os pontos: \begin{matrix} (0,1) &,& (0,3) &,& (1,0) &,& (2,0) \end{matrix}Esses pontos determinam uma área $(S)$ que pode ser calculada pela subtração da área de dois triângulos retângulos, veja a figura no final da segunda resolução: \begin{matrix} S = \dfrac{2\cdot 3}{2} - \dfrac{1\cdot 1}{2} &\therefore& \fbox{$S = \dfrac{5}{2}$} \end{matrix}$• \ \text{Resolução II:}$ Ao observar o conjunto do enunciado, pode-se pensar numa equação quadrática em $x$ ou $y$, a rigor façamos em $x$ : \begin{matrix} 3x^2 +x(5y-9) + 2(y^2-4y+3) = 0 &\Rightarrow & \Delta = (y+3)^2 &,& x = \dfrac{(9-5y) \pm (y+3)}{6} \end{matrix}Constata-se: \begin{matrix} (x+y-1)(3x+2y-6) = 0 \end{matrix}A partir daqui o raciocínio é análogo, \begin{matrix} Letra \ (B) \end{matrix}