Uma pequena pedra repousa no fundo de um tanque de de profundidade. Determine o menor raio de uma cobertura circular, plana, paralela à superfície da água que, flutuando sobre a superfície da água diretamente acima da pedra, impeça completamente a visão desta por um observador ao lado do tanque, cuja vista se encontra no nível da água. Justifique.
Dado: índice de refração da água $\displaystyle n_w=\frac{4}{3}$
$-$ Para que o observador não consiga ver a pedra no fundo do tanque, deve de haver $\text{Reflexão Total}$, assim:
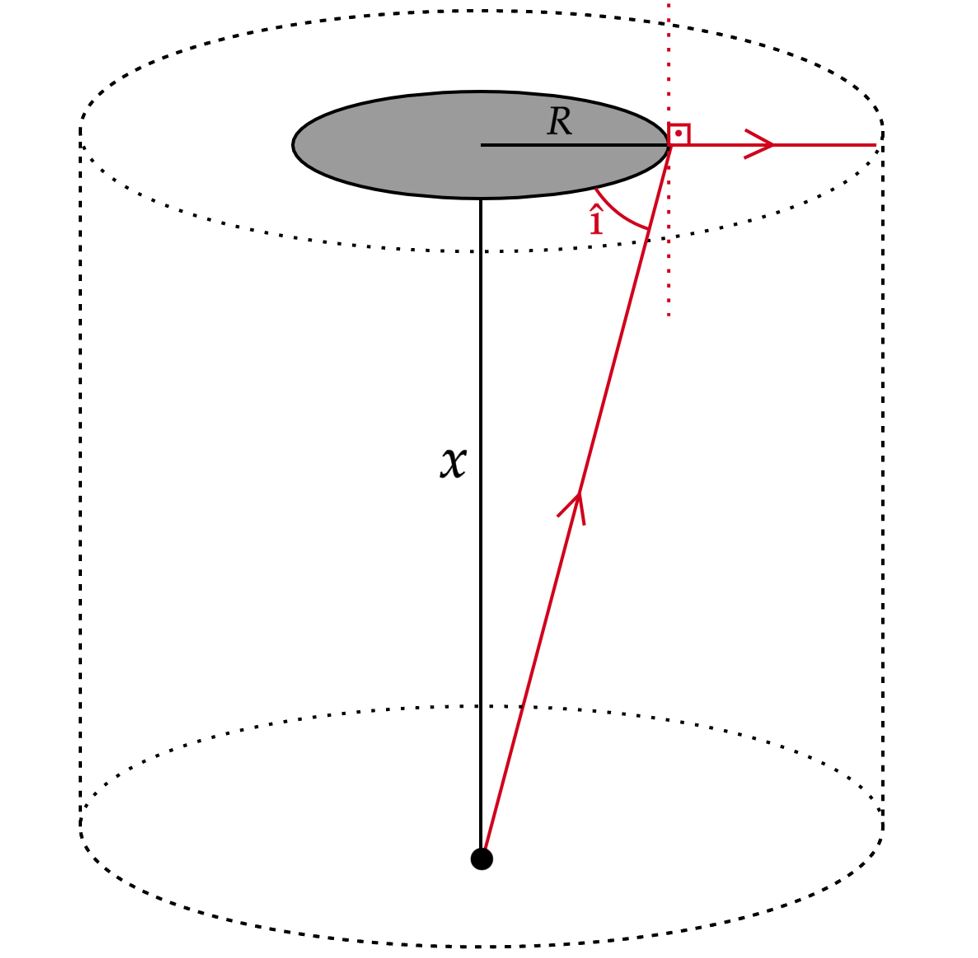\begin{matrix} \Large{\frac{\sin{(90^{\circ} - î)}}{\sin{90^{\circ}}} = \frac{n_{ar}}{n_w}} &\Rightarrow& \sin{(90^{\circ} - î)} = \large{\frac{3}{4}}
\end{matrix} $-$ A partir do $\text{Teorema de Pitágoras}$, temos
\begin{matrix}\sin{(90^{\circ} - î)}= \large{\frac{3}{4}} = \large{\frac{R}{\sqrt{x^2 + R^2}}} &\Rightarrow& \fbox{$R = \Large{\frac{3x\sqrt{7}}{7}}$}
\end{matrix}
Ampliar Imagem
