Uma massa é liberada a partir do repouso de uma altura acima do nível do solo e desliza sem atrito em uma pista que termina em um “loop” de raio , conforme indicado na figura.
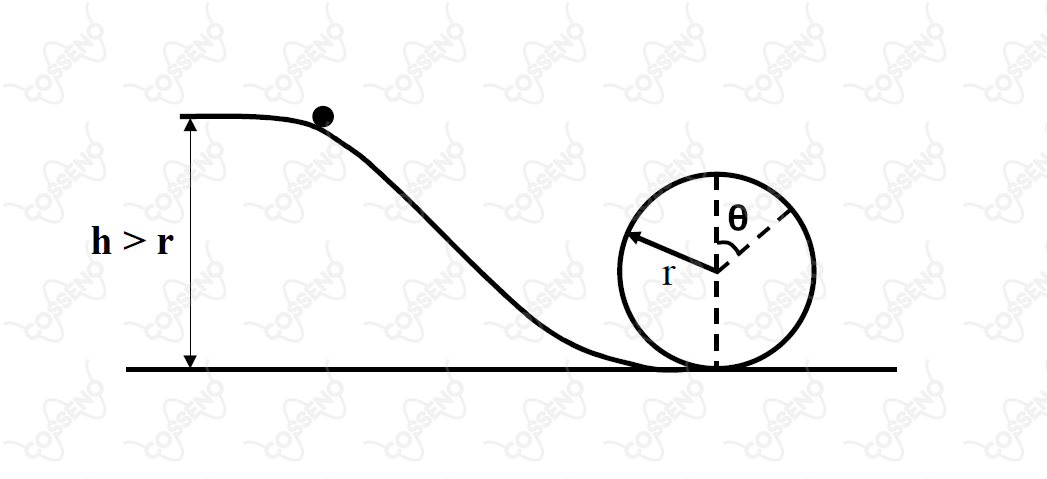
Determine o ângulo relativo à vertical e ao ponto em que a massa perde o contato com a pista. Expresse sua resposta como função da altura , do raio e da aceleração da gravidade .
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Conservando a energia mecânica:
$$mgh = mgr(1+\cos \theta) + \dfrac{mv^{2}}{2} \ \Leftrightarrow \ \dfrac{v^{2}}{2} = g[h - r(1 + \cos \theta)].$$
Para encontrar a velocidade, basta um pouco da dinâmica do movimento curvilíneo, fazendo $N = 0$, pois é dito que o corpo perde o contato com pista.
$$\dfrac{mv^{2}}{r} = mg\cos \theta \ \Leftrightarrow \ \dfrac{v^{2}}{2} = \dfrac{gr\cos \theta}{2}.$$
Substituindo a equação encontrada na primeira,
$$\dfrac{gr\cos \theta}{2} = g[h - r(1 + \cos \theta)] \ \Leftrightarrow \ r\cos \theta = 2h - 2r - 2r\cos \theta \ \Leftrightarrow \ \theta = \arccos \left[\dfrac{2(h-r)}{3r}\right].$$

