Um corpo de massa , mostrado na figura, é preso a um fio leve, inextensível, que passa através de um orifício central de uma mesa lisa. Considere que inicialmente o corpo se move ao longo de uma circunferência, sem atrito.
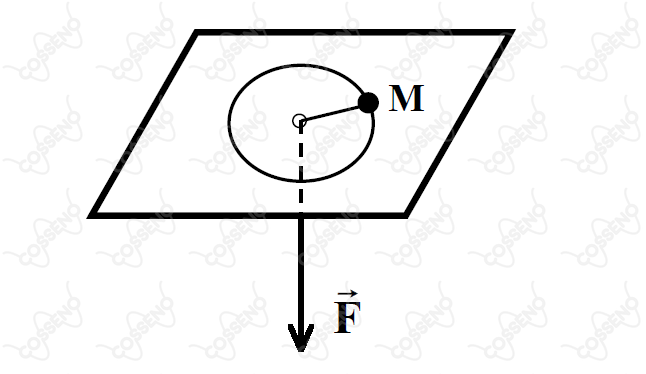
O fio é, então, puxado para baixo, aplicando-se uma força , constante, a sua extremidade livre. Podemos afirmar que:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

$• \ \text{Alternativa (A):}$ $\color{orangered}{\text{Incorreta}}$
O fio será puxado, ou seja, o corpo será arrastado para dentro conforme o movimento do fio. Consequentemente, não permanecerá ao longo da mesma circunferência.
$• \ \text{Alternativa (B):}$ $\color{orangered}{\text{Incorreta}}$
Com o fio sendo puxado uma distância $d$ para baixo, o trabalho realizado pela força $F$ será: $W_F= F\cdot d$
$• \ \text{Alternativa (C):}$ $\color{orangered}{\text{Incorreta}}$
Visto que o trabalho não é nulo, certamente a potência instantânea também não será.
$• \ \text{Alternativa (D):}$ $\color{#3368b8}{\text{Correta}}$
Observe que a força $F$ é externa ao sistema, valendo-se então do $\text{teorema da energia cinética}$, em que:\begin{matrix}
W_F = \Delta E_c
\end{matrix}Portanto, o resultado segue.
$• \ \text{Alternativa (E):}$ $\color{orangered}{\text{Incorreta}}$
O movimento não será necessariamente elíptico, mas sim curvilíneo. No caso, devido a ação da força $F$, nota-se que o corpo irá adquirir velocidade radial, sendo sua trajetória próxima das $\text{Espirais de Arquimedes}$.\begin{matrix}Letra \ (D)
\end{matrix}

