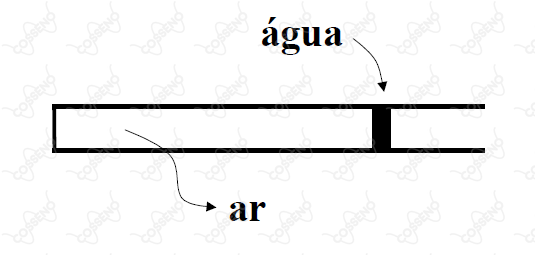
Um tubo capilar fechado em uma extremidade contém uma quantidade de ar aprisionada por um pequeno volume de água. A e à pressão atmosférica () o comprimento do trecho com ar aprisionado é de . Determine o comprimento do trecho com ar aprisionado a . Se necessário, empregue os seguintes valores da pressão de vapor da água: a e a .
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Em tese, estamos lidando com duas situações de equilíbrio, uma à $7 \ \pu{ºC}$ e outra à $17 \ \pu{ºC}$. Mais precisamente, em ambas as situações há o equilíbrio entre as forças; da atmosfera, do ar e do vapor d'água sobre o volume de água. Tanto a força do ar quanto a do vapor são internas, por outro lado, a força da atmosfera é externa, o que nos permite equacionar:\begin{matrix}
F_{atm} = F_{Ar} + F_{Vapor}
\end{matrix}Como a gota está aprisionando o ar, esta deve apresentar mesma seção transversal $A$ do tubo capilar. Assim, com conhecimento que força é, basicamente, pressão sobre área, podemos escrever:\begin{matrix}
A \cdot P _{atm} = A \cdot P_{Ar} +A \cdot P_{Vapor}
\end{matrix}Então,\begin{matrix} P_{Ar} = P _{atm} - P_{Vapor}
\end{matrix}Repare que a pressão da atmosfera deve ser invariável, ou seja, para cada situação, têm-se: \begin{matrix}
7 \ \pu{ºC} &:& P_{Ar, 7 \ \pu{ºC} } = 76,0 - 0,75 &\therefore& P_{Ar, 7 \ \pu{ºC} } = 75,25 \ \pu{cm Hg}
\\
17 \ \pu{ºC} &:& P_{Ar, 17 \ \pu{ºC} } = 76,0 - 1,42 &\therefore& P_{Ar, 17 \ \pu{ºC} } = 74,56 \ \pu{cm Hg}
\end{matrix}Admitindo o comportamento ideal dos gases, pela equação geral dos mesmos, têm-se:\begin{matrix}
\dfrac{P_{Ar, 17 \ \pu{ºC} } \cdot V_{ 17 \ \pu{ºC} } }{T_{ 17 \ \pu{ºC} } } = \dfrac{P_{Ar, 7 \ \pu{ºC} } \cdot V_{ 7 \ \pu{ºC} } }{T_{ 7 \ \pu{ºC} } }
\end{matrix}Consequentemente,\begin{matrix}
\dfrac{74,56 \cdot (A \cdot L)}{280} = \dfrac{75,25 \cdot (A \cdot 15)}{290} &\therefore& L \approx 15,67 \ \pu{cm} \ \ \tiny{\blacksquare}
\end{matrix}$\color{orangered}{\text{Obs:}}$ Não se esqueça de converter a temperatura para kelvin na equação acima.

