Uma rampa rolante pesa e se encontra inicialmente em repouso, como mostra a figura. Um bloco que pesa , também em repouso, é abandonado no ponto , deslizando a seguir sobre a rampa. O centro de massa da rampa tem coordenadas: e . São dados ainda: e . Desprezando os possíveis atritos e as dimensões do bloco, pode-se afirmar que a distância percorrida pela rampa no solo, até o instante em que o bloco atinge o ponto , é 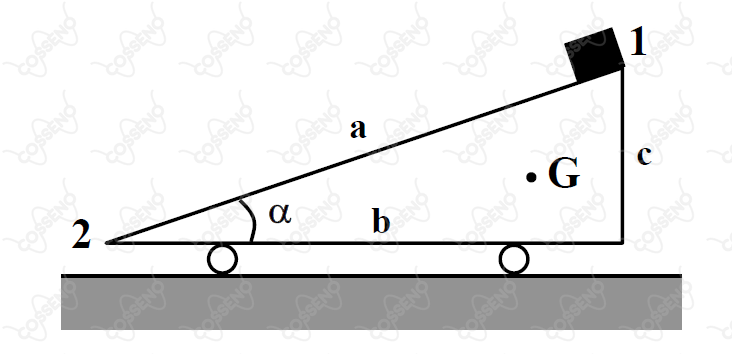
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Pensando na geometria da rampa, pode-se escrever que: \begin{matrix}
\sin{\alpha} = \dfrac{c}{a} &\Rightarrow& \boxed{c = 9 \ \pu{m}} &\overset{\text{cf. Pitágoras}}{\therefore}& \boxed{b = 12 \ \pu{m}} &\because& a^2 = b^2 + c^2
\end{matrix}Analisando o sistema rampa-bloco, nota-se que ele é isolado na horizontal, com isso, pela quantidade de movimento do sistema, têm-se: \begin{matrix}
p_{sistema} = 0 &\Leftrightarrow& 8\cdot v_b + 12 \cdot v_r = 0&|& v_b = \dfrac{\Delta x_b}{\Delta t} &,& v_r = \dfrac{\Delta x_r}{\Delta t}
\end{matrix}Para um mesmo intervalo de tempo, têm-se: \begin{matrix}
(1): & 8 \cdot \Delta x_b +12 \cdot \Delta x_r = 0 &|& \Delta x_b = (x_{bf} - x_{bi}) &,&\Delta x_r = (x_{rf} - x_{ri})
\end{matrix}Adotando um par de eixos coordenados conveniente, pode-se pensar no movimento como:
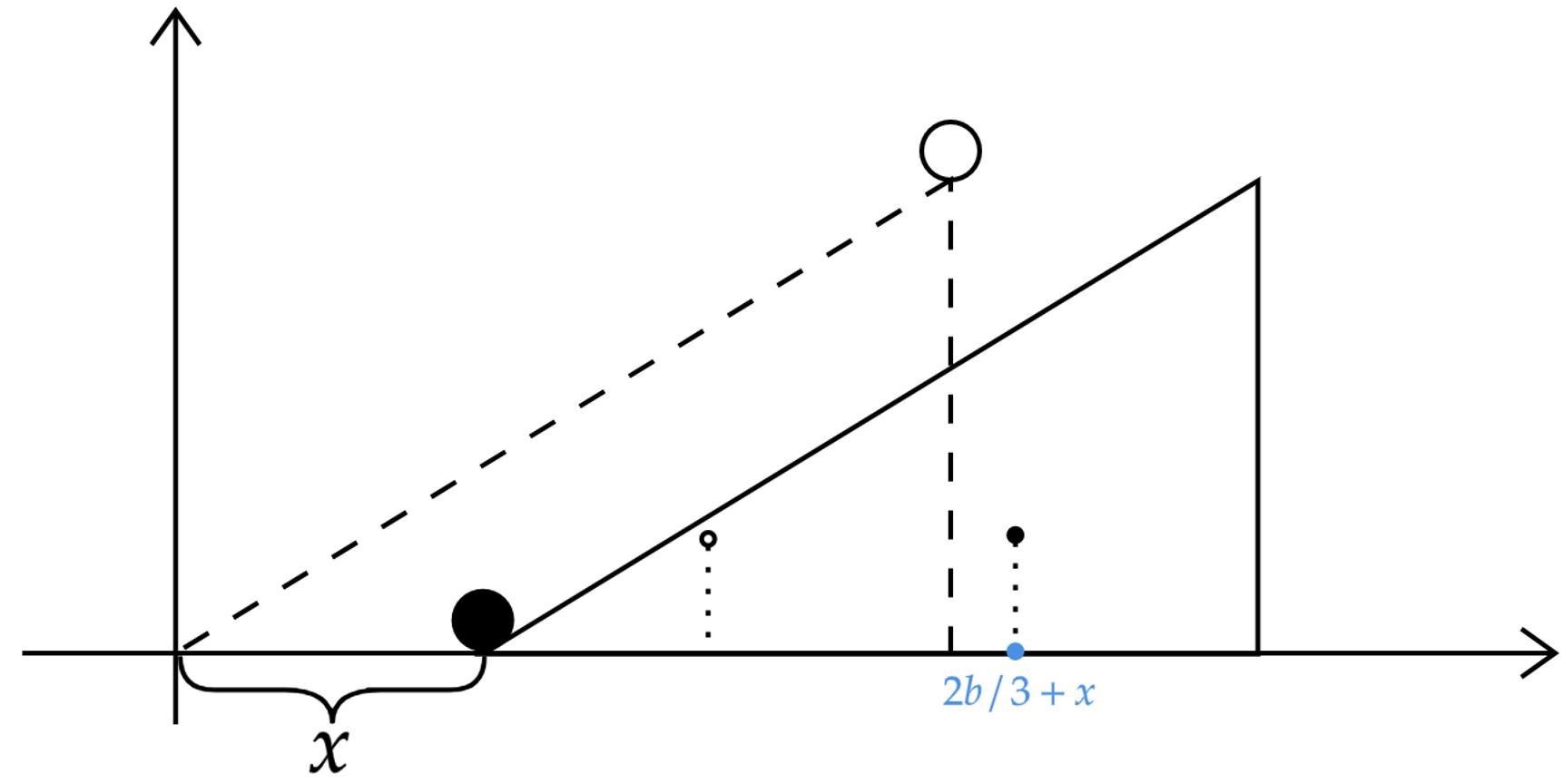 Não é difícil perceber que: \begin{matrix}
x_{bf} = \dfrac{2b}{3} + x &,& x_{bi} = \dfrac{2b}{3} &,& x_{rf} = x &,& x_{ri} = b
\end{matrix}Com isso, a partir de $(1)$: \begin{matrix}
8 \cdot (x - b) + 12 \cdot \left(\dfrac{2b}{3} + x - \dfrac{2b}{3} \right) = 0&\Rightarrow& 20x = 8b &\therefore& x = 4,8 \ \pu{m} &\tiny{\blacksquare}
\end{matrix}\begin{matrix} Letra \ (C)
\end{matrix}$\color{orangered}{Obs:}$ Um processo de resolução análogo seria pelo centro de massa do sistema. Além disso, repare que $\Delta x_r = x$.
Não é difícil perceber que: \begin{matrix}
x_{bf} = \dfrac{2b}{3} + x &,& x_{bi} = \dfrac{2b}{3} &,& x_{rf} = x &,& x_{ri} = b
\end{matrix}Com isso, a partir de $(1)$: \begin{matrix}
8 \cdot (x - b) + 12 \cdot \left(\dfrac{2b}{3} + x - \dfrac{2b}{3} \right) = 0&\Rightarrow& 20x = 8b &\therefore& x = 4,8 \ \pu{m} &\tiny{\blacksquare}
\end{matrix}\begin{matrix} Letra \ (C)
\end{matrix}$\color{orangered}{Obs:}$ Um processo de resolução análogo seria pelo centro de massa do sistema. Além disso, repare que $\Delta x_r = x$.

Ampliar Imagem

