Num sistema de coordenadas cartesianas, duas retas $r$ e $s$ , com coeficientes angulares $2$ e $\frac{1} {2}$ , respectivamente, se interceptam na origem $0$ . Se $B \in r$ e $C \in s$ são dois pontos no primeiro quadrante tais que o segmento $\overline{BC}$ é perpendicular a $r$ e a área do triângulo $OBC$ é igual a $12 \times {10}^{-1}$ , então a distância de $B$ ao eixo das ordenadas vale
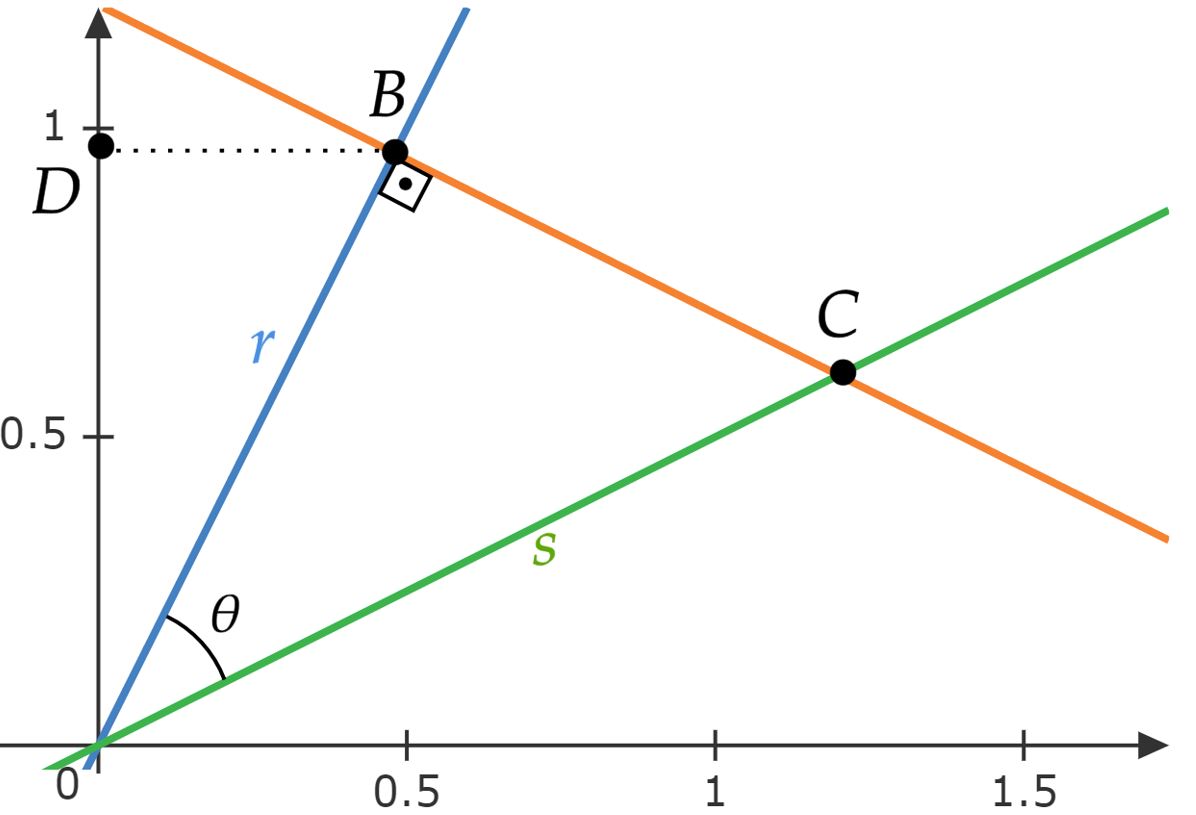
$• \ \text{Resolução I:}$ Denotemos os pontos $B:(a,b)$ e $C:(c,d)$, assim, a partir dos coeficientes angulares das retas não é difícil encontrar a equação reduzida das mesmas: \begin{matrix} r: \ y = 2x &\Rightarrow& \fbox{$b =2a$} &&,&& s: \ y = \dfrac{1}{2}x &\Rightarrow& \fbox{$c =2d$}
\end{matrix}Utilizando o algoritmo de área da geometria analítica: \begin{matrix} \Delta &=&\begin{vmatrix} 0 &0\\ a&b \\ c&d \\ 0&0
\end{vmatrix} &=& ad -bc &&,&& \dfrac{1}{2}|\Delta| = 12\cdot 10^{-1} & \text{(I)}
\end{matrix}Segundo enunciado, por $\overline{BC}$ constatamos o coeficiente angular da reta como $m =-\frac{1}{2}$, visto que $r$ e o segmento são perpendiculares. Nesse viés, com conhecimento de $m$, têm-se: \begin{matrix} m = {\dfrac{(b-d)}{(a-c)}} &\Rightarrow& c-a =2b -2d &\therefore& \fbox{$d = {\dfrac{5a}{4}}$} &\Rightarrow& \fbox{$c = {\dfrac{5a}{2}} $}
\end{matrix}Substituindo nossos resultados em $\text{(I)}$: \begin{matrix} \dfrac{1}{2}|ad -bc| = 12\cdot 10^{-1} &\therefore& \fbox{$a = {\dfrac{4}{5}} $}
\end{matrix}Não é complicado perceber que, a distância de $B$ ao eixo das ordenadas vale $a$.
$• \ \text{Resolução II:}$ No começo da resolução anterior, atente que $B:(a,2a)$, nessa perspectiva, vejamos o ângulo formado entre $r$ e $s$ , chamemos de $\theta$:\begin{matrix} \tan{\hat{r}} = 2 &,& \tan{\hat{s}}= \dfrac{1}{2} &,& \theta = \hat{r} - \hat{s} &\Rightarrow& \tan{\theta} = {\dfrac{ \tan{\hat{r}}- \tan{\hat{s}}}{1+ \tan{\hat{r}}\cdot \tan{\hat{s}}}} &\therefore& \tan{\theta} = \dfrac{3}{4}
\end{matrix}Veja que, o triângulo $OBC$ é retângulo, vide $\overline{BC}$ ser perpendicular a $r$. Por isso, a área do triângulo pode ser escrita como:\begin{matrix} {\dfrac{\overline{BC}.\overline{OB}}{2} }&=& { \dfrac{(\overline{OB})^2\cdot \tan{\theta}}{2}} &=& 12\cdot 10^{-1} &\therefore& (\overline{OB})^2 = \large{\frac{16}{5}}
\end{matrix}Novamente, identifique outro triângulo retângulo, ele será formado pelos pontos $O:(0.0)$, $D:(a,0)$ e $B:(b,2b)$, em que $\overline{DB}=a$ e $\overline{OD}=2a$ . Por fim, aplicando o teorema de Pitágoras:\begin{matrix} (\overline{OB})^2 = (\overline{BD})^2 + (\overline{OD})^2 &\therefore& \fbox{$a = {\dfrac{4}{5}} $}
\end{matrix}
\begin{matrix}Letra \ (B)
\end{matrix}
Ampliar Imagem
